Emergence of Peregrine solitons in integrable turbulence of deep water gravity waves

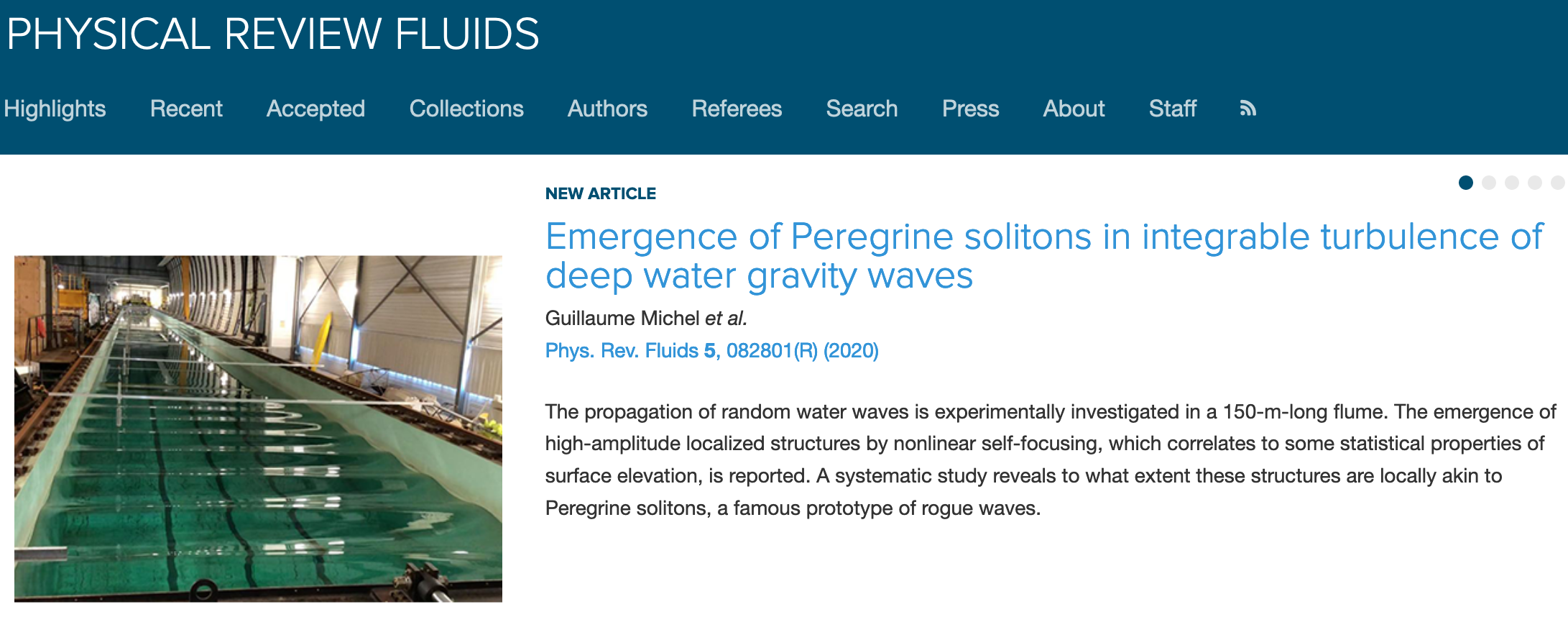
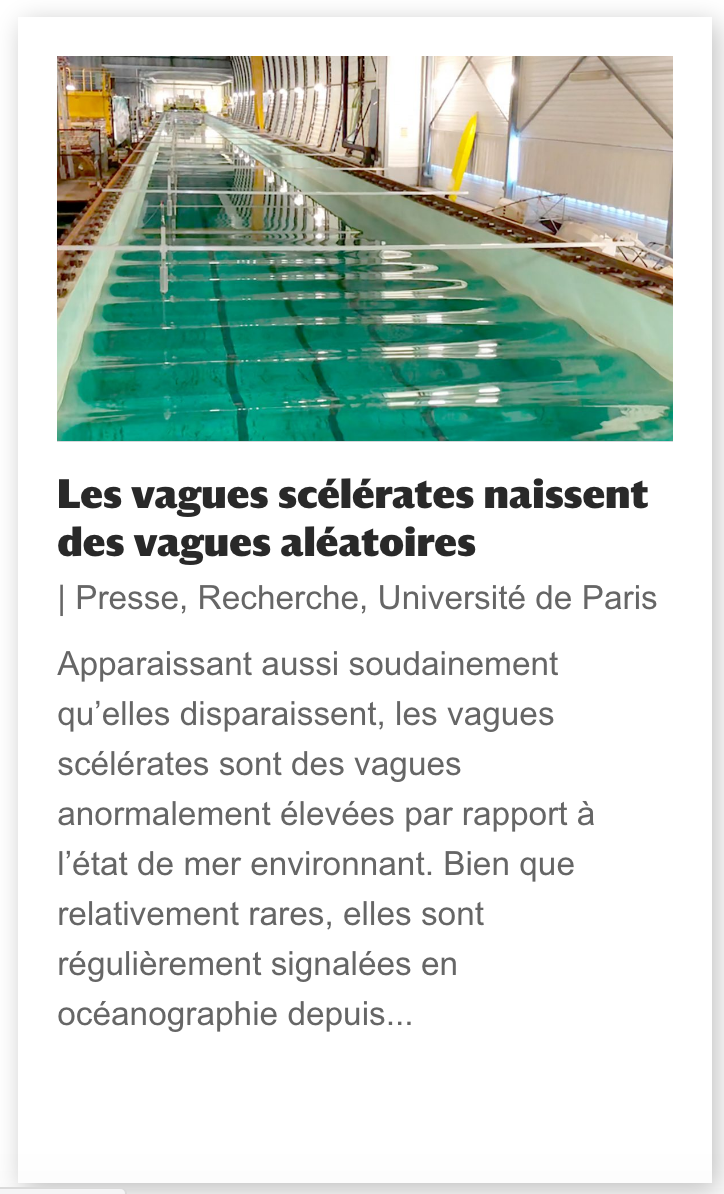
Abstract: We study experimentally the early stages of integrable turbulence of unidirectional deep water gravity waves. By generating partially coherent waves in a 148-m-long wave flume, we observe the emergence of high-amplitude structures formed by nonlinear focusing, commonly referred to as rogue waves. This work confronts the experiment with two recent results obtained in the framework of the nonlinear Schrödinger equation (NLSE), namely that (i) these structures can be locally fitted by a Peregrine soliton and (ii) their emergence leaves a visible trace on the evolution of statistical parameters such as kurtosis. We show that (i) yields accurate results as long as the wave steepness remains moderate, whereas (ii) is very robust and remains valid beyond the assumption of integrability. Numerical simulations of the NLSE and of the fully nonlinear dynamical equations are also performed to support these results.

PDF file

''How are rogue waves born?'' in The Conversation 27 Sept. 2020 (in french by E. Couderc/G. Michel)

  "Rogue waves are born out of random waves" in CNRS Research News 11 Sept. 2020 (in french),       

  Les vagues scélérates naissent des vagues aléatoires, in Université de Paris Infos, August 28, 2020 (in french)  (or see PDF )

    Les vagues scélérates naissent des vagues aléatoires MSC Laboratory Web Site, September 11, 2020 (in french)