L’origine des tétrapodes, en résumé.
La formation des embryons de vertébrés passe par un ensemble de mouvements hydrodynamiques, ayant lieu dans les jeunes embryons, au stade où ils sont des sphères ou des disques. L’embryon lui-même occupe une partie de ce disque, l’autre partie formant les « organes extra-embryonnaires ».
Par hydrodynamique, il faut entendre qu’il s’agit d’un écoulement d’un matériau visqueux, soumis à des forces de volume dues à la traction par les cellules elles-mêmes. Le fait que des cellules soient parties prenantes d’un matériau, qu’elles soient au contact les unes avec les autres, a pour conséquence que tout déplacement d’une cellule est en interaction avec les autres, pour la même raison que si on tire sur un drap d’un côté, ça bouge à l’autre bout. Cet interaction est indépendante de la chimie, il s’agit de l’écriture de la loi physique d’équilibre du matériau sous l’effet du déplacement d’une cellule. De même qu’une plaque horizontale (étagère) fléchit quand on pose un livre dessus, une plaque horizontale (embryon) se déforme dans son plan, quand on tire dans son plan. Dans le cas particulier des matériaux visqueux, une traction localisée (une cellule), induit un dipôle de déplacement aux alentours. Trouver le mouvement global requiert de sommer tous les dipôles résultant de toutes les interactions entre cellules, et de traiter le mouvement des forces elles-mêmes, dans l’écoulement qu’elles s’imposent à elles-mêmes.
Les écoulements dans les jeunes embryons ont été historiquement décrits de façon erronée, comme par exemple dans
(Ajout 2012 : j'avais extrapolé cette affirmation d'articles récents citant cette figure. Entretemps, je suis allé voir l'article original de Wetzel et ai trouvé une autre figure qui montre un écoulement vers l'arrière, donc la présence d'un point-col très "caudal", la dite figure de Wetzel est montrée ici http://www.msc.univ-paris-diderot.fr/~vfleury/portailtourbillons.html; de nos jours, les mesures par PIV ont précisé la position et l'auto-organisation de ce point col).
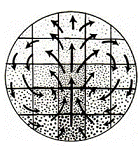
D’après R. Wetzel, Untersuchungen am Hühnchen. Die Entwicklung
des Keims während der ersten beiden Bruttage, Arch. Entw. Mech. Org.
119, 188 (1929).
En réalité, comme décrit pour la première fois dans (V. Fleury, Organogenesis, 2, 1, 6 2005 et V. Fleury, Revue des Questions Scientifiques, 177, 3-4, 235 (2006)), les écoulements dans les jeunes embryons présentent un point col, avec un écoulement vers l’arrière ET vers l’avant.
Un point col est un point de vitesse nulle, séparant quatre domaines où les lignes de courant recirculent avec des vorticités opposées (+,-,+,-) (ça tourne à l’envers, quand on passe d’un cadran à l’autre).
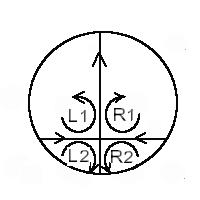
Les vorticités sont
opposées, en passant d’un cadran à l’autre, en raison des lois de conservation
de l’hydrodynamique au voisinage d’un point col (ça tourne « dans le sens
opposé des aiguilles d’une montre » en L1, puis dans le sens des Ad’uneM en R1 puis en sens opposé des Ad’uneM
en R2 puis dans le sens des Ad’uneM en L2.
Je pense que le fait même qu’il y ait un écoulement vers l’arrière était tellement difficile à comprendre intellectuellement, que les chercheurs du passé n’insistaient pas sur cet écoulement, ou même ne « le voyaient pas ». Cette tendance est éminemment perceptible dans les travaux actuels, qui voient l’écoulement hyperbolique avec un point col, mais centrent toujours les images ailleurs. Le point col est la plupart du temps difficile à voir étant toujours « sur le bord » de l’image. Par exemple dans :
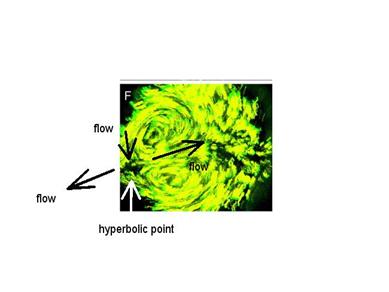
D’après : C. Cui, X. Yang, M. Chuai,
J. A. Glazier, C. J. Weijer, Dev.
Biol. 284, 37
(2005). Imagerie par fluorescence de trajectoires cellulaires montrant le point
col, sur le bord. J’ai rajouté les flèches.
et dans :
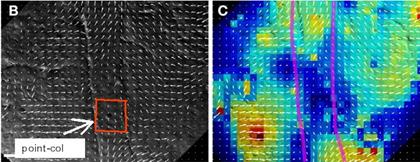
D’après, Cooperation of polarized cell
intercalations drives convergence and extension of presomitic mesoderm during zebrafish gastrulation, Chunyue
Yin, Maria Kiskowski,
Philippe-Alexandre Pouille, Emmanuel Farge, and Lilianna Solnica-Krezel, The Journal of Cell Biology, Vol. 180, No. 1, 221-232. le point col est
parfaitement visible ici, je l’ai entouré en rouge.
et dans :

The ECM Moves during Primitive Streak Formation—Computation of ECM
Versus Cellular Motion Evan A. Zamir¤, Brenda J. Rongish, Charles
D. Little PLOS biology 2008
Ce point col existe bien ; par conséquent, la vision habituelle de l’embryologie, selon laquelle les animaux sont formés de façon antéro-postérieure est erronée, et même, caduque. La description faite récemment par Chuai et Weijer, en termes d’un dipôle est également erronée.
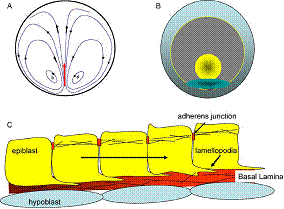
Description
de l’écoulement à l’aide
d’un dipôle hydrodynamique
(The Mechanisms Underlying Primitive
Streak Formation in the Chick Embryo Manli Chuai and Cornelis
J. Weijer, Curr Top Dev Biol
81: 135-56, 2007).
En réalité, les embryons de vertébrés se
forment à partir d’un système quadru-polaire, dont le
schéma le plus simple, donné dans (V. Fleury, Organogenesis, 2, 1, 6 2005) est :
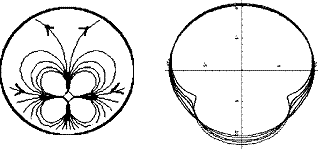
L’image de gauche
donne le champ de vitesse, l’image de droite, la déformation progressive du
disque-embryon. Cet écoulement est obtenu en supposant que les cellules du
croissant de Koller-Rauber
tirent. Ce croissant de Koller-Rauber
est une région en forme de croissant, héritée de la rotation corticale de
l’ovocyte et des premières divisions cellulaires qui est présente dans une
région basse du disque, qui sera finalement le nombril.
Le champ de vitesse créé
par une cellule unique est de la forme (avec un préfacteur
tenant compte de la viscosité et de l’épaisseur)
v=rot(Y(x,y)), avec Y (x,y)=x/x2+y2,
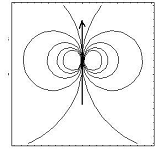
Champ dipôlaire de la forme v=rot(x/x2+y2),
créé par une force concentrée en (0,0)
en sorte
qu’un quadru-pôle est de la forme (x-a)/(x-a)2+(y)2
–(x+a)/(x+a)2+(y)2. La valeur de a étant le centre du
vortex, ou l’extrémité du segment qui tire. Il s’agit d’un quadru-pôle
singulier au point col obtenu en supposant le croissant qui tire très fin. On
peut relaxer cette contrainte et supposer la région qui tire un peu plus large,
formant en quelque sorte un rectangle, moyennant quoi, il faut intégrer cette
fonction sur la région qui tire. On trouve alors un écoulement de la forme
v=rot(Y (x,y), avex Y (x,y)= òr1r2 (x-a)/(x-a)2+(y-b)2 da-
òr3r4 (x-a)/(x-a)2+(y-b)2da
~Ln(r1)-Ln(r2)-(Ln(r3)-Ln(r4)), où r1, r2, r3 et r4 sont les distances
rapportées au centre des vortex, qui correspondent aux limites de la zone qui
tire.
Techniquement, cela revient à
relaxer la singularité au point col, le point col quadru-polaire
étant obtenu comme limite lorsque les centres M1 et M2 et M3 M4 des vortex se
rapprochent. De façon plus figurative, les lignes de courant prennent la
forme :


Comme décrit dans mon article (V. Fleury, Revue des Questions
Scientifiques, 177, 3-4, 235 (2006)), et repris dans V. Fleury, A. Al-Kilani,
M. Unbekandt and T.-H. Nguyen, Organogenesis, 3,
1, 49 (2007). Au droite une image obtenue dans l’équipe de Cornelis Weijer à
Dundee.
Comme on le voit sur la
figure (et précisé dans les articles), il n’est pas nécessaire d’observer des
tourbillons entiers : en raison du théorème-image, les écoulements peuvent
virtuellement exister à l’extérieur de l’objet, l’objet lui-même étant entouré
par une frontière libre qui se déplace dans l’écoulement (d’où les simulations
dans les articles de formes d’embryon, qui me semblent être les premières du
genre (pardon, les secondes, il y a un papier historique de A. G. Jacobson and
R. Gordon, The Journal of experimental zoology, 197, 2 (1976), absolument stupéfiant montrant des
images un peu du même genre). Par ailleurs, le paradoxe de Stokes-Whitehead
implique que les tourbillons sont nécessairement faux au voisinage de la
singularité, puisque la vitesse y diverge, ce qui n’est pas physique (il faut ré-introduire les termes d’advection dans l’équation de
Stokes).
Par ailleurs, si l’on suppose que toutes les cellules se
mettent peu à peu à tirer (et non seulement le croissant de Koller-Rauber), on obtient comme solution des tourbillons dits
« de coeur solide » ; c’est un calcul
très facile, il suffit de prendre une force uniforme tirant dans l’écoulement
(voir Clarifying tetrapod embryogenesis and evolution, a physicist’s point of view,
Vincent Fleury, à paraître).
A partir de ce modèle, on comprend parfaitement la formation
des animaux (vertébrés tétrapodes).
Tout
d’abord, il faut noter qu’il s’agit ici d’une description en écoulement
stationnaire. Or l’hydrodynamique nous enseigne que ces tourbillons ne peuvent
JAMAIS être stationnaires (voir par exemple le cours de Paterson, First course
in Hydrodynamics, Cambridge University
Press, 1988). Ceci explique pourquoi les expériences
voient des tourbillons plus ou moins bien formés, pas toujours pareils :
il y a une instationnarité, les tourbillons se déplacent, comme se déplacent des ronds
de fumée (« comme » étant au sens strict, la seule différence est que
les ronds de fumée ne sont pas entretenus, une fois émis par la bouche du
fumeur -voir par exemple : The decay of a viscous vortex pair, Brian Cantwell
and Nicholas Rott, Physics
of Fluids, 31, 11, November
1988).
Ce déplacement est pris en
compte dans V. Fleury, Revue des Questions Scientifiques, 177, 3-4, 235 (2006),
en tenant compte du fait que les équations de l’hydrodynamique montrent qu’une
singularité tourbillon se déplace dans le champ de vitesse créé par les autres.
On trouve alors que les tourbillons s’enroulent vers l’avant, et vers
l’arrière, en s’éloignant d’un point col (immobile) qui constituera finalement
le nombril. Un calcul simple donne :
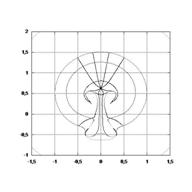
Par conséquent, l’enroulement entraine les tissus contre le corps, et les
fait lever par un effet mécanique (l’enroulement crée un gradient de contrainte
orienté du corps vers le coeur de l’enroulement, la
croissance a lieu dans le sens du gradient de contrainte). Un point intéressant
est que ce modèle explique très simplement pourquoi certains animaux ont des
pattes et d’autres pas : l’enroulement crée une localisation des gradients
qui est susceptible, ou pas, de permettre l’extension ensuite de la patte. Il
va de soi qu’en l’absence complète de tourbillon, l’animal aura juste une queue
en pointe sans pattes, mais que les pattes seront de plus en plus
« présentes », à proportion de la quantité d’enroulement effectivement
présente. Le gradient de force apparaît dans les zones enroulées, il n’est
évidemment pas nécessaire qu’un tourbillon entier soit présente, de même que
dans un bécher tournant, l’ensemble de la surface se déforme, on peut isoler
par la pensée la surface d’« un quart de bécher », elle est également
déformée (ceci pour couper court à des propos diffamatoires à mon encontre). En
ce sens, les animaux ont tous virtuellement des pattes, j’utilise fréquemment
le mot « latentes », les pattes sont « latentes », et, dans
le sens de l’évolution, l’enroulement aura tendance à faire apparaître des
pattes, puis à les faire disparaître (serpents) si l’enroulement est trop étiré
dans le sens tête-queue.
Un point mérite d’être
souligné :
L’enroulement n’est bien entendu
pas terminé au stade où des champs de vitesse comme :

D’après X. Yang, D. Dormann, A. E. Münsterberg, and C. J. Weijer, Developmental
Cell, 3, 425 (2002). le point col est représenté par
le carré rouge.
sont montrés dans
la littérature récente. Le mouvement continue, puisqu’en réalité, toute la
formation de l’animal n’est qu’un grand enroulement-aplatissement unique.
Pour comprendre le mouvement il
faut suivre le film par la suite, comme par exemple le film que nous avions
produit avec Ferdinand pour notre article (F. LeNoble, D. Moyon, L. Pardanaud, L. Yuan, V. Djonov, R.
Mattheijssen, C. Bréant, V. Fleury and A. Eichmann, Development, 131, 361 (2004).
voir supplementary material).
Peu à peu l’animal s’allonge,
tandis que les plaques latérales se rapprochent et gauffrent
jusqu’à temps que les pattes commencent à saillir.
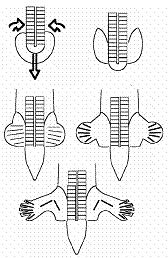
Schéma de la sortie des pattes arrières.
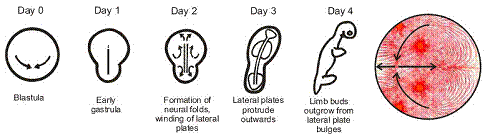
Schéma pour l’embryon dans
son ensemble. A droite : un calcul plus proche des écoulements réellement
observés, en positionnant mieux la
position initiale des tourbillons (ce qui revient à prendre un arc pour le
croissant de Koller, au lieu d’une barre
horizontale).
L’enroulement pendant formation
des plaques latérales par où vont saillir les pattes est très évidente sur
toutes sortes de marquages comme ci-dessous le marquage de Tbx4, ou l’image en shadowgraph montrant l’enroulement qui
est sur mon site, avec la levée concomitante de la plaque latérale

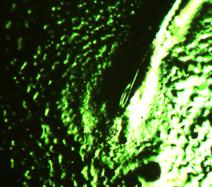
Voir aussi (le dernier article de Kees Weijer, où il me semble que l’enroulement est très
visible, j’attends confirmation)
Pour finir, il faut indiquer que,
au voisinage du point col, la fonction de courant se simplifie en Y(x,y)= kxy, en sorte que l’écoulement est de la forme v(x,y)=(-kx,ky) (développement
limité de quatre tourbillons, développés au voisinage du centre hyperbolique).
Dans ce cas, l’écoulement est élongationnel,
c’est-à-dire qu’il ne fait que transformer des formes de façon affine, en les
comprimant dans un sens et dilatant dans l’autre (d’où le vocable
« extension convergente »).
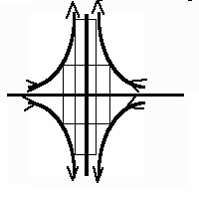
Image
du transport dans un écoulement hyperbolique. les lignes de courant sont es
hyperboles, e l’écoulement est élongationnel :
il ne fait qu’allonger dans un sens, et aplatir dans l’autre, bien que chaque
point suive une trajectoire hyperbolique (« streakline »,
à ne pas confondre avec « streamline »).
Cette vision est ce qu’on appelle en physique la version lagrangienne de
l’écoulement, par opposition à la version eulerienne.
La conséquence
de ce pattern particulier d’écoulement, est que les champs de concentration
suivent le rétrécissement dans un sens et l’allongement dans l’autre
passivement comme observé :
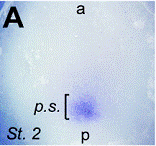
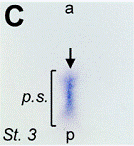
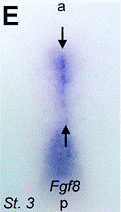
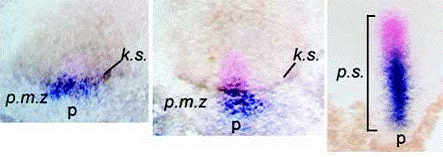
Images d’allongements des patterns d’expression dans l’écoulement
hyperbolique (d’après T. Mikawa, A. Poh,
K. Kelly, Y. Ishii, and D. Reese,
Developmental dynamics,
229, 422
(2004),
et D. L. Chapman, N. Garvey, S. Hancock, M. Alexiou,
S. I. Agulnik, J. Thomas, R. J. Bollag,
L. M. Silver, and V. E. Papaioannou,. Dev. Dyn. 206, 379 (1996).
L’écoulement transforme donc en fait le terme de source du mouvement (la
zone marquée dans la région du croissant de Koller-Rauber) d’une façon self-consistante avec le transport hydrodynamique
dans des tourbillons transportés eux-mêmes par l’écoulement qu’ils s’infligent
à eux mêmes, ce qui clôt mathématiquement le système.
Voilà. Si vous avez tout
compris jusqu’ici, vous avez compris, en gros, que les vertébrés tétrapodes ne sont
pas le « fruit du hasard », mais l’attracteur hyperbolique d’un
mouvement hydrodynamique auto-cohérent, qui est emporté depuis sa condition
initiale vers un pattern allongé, cintré, avec quatre pattes. C’est très
simple.