|
In thisd page I propose several problems on which I have unfortunately not enough time to work.
If you have any interest in any of these problems, you are welcome to contact me to interact,
or just give me the solution if you know it, I would be very pleased.
|
|
Problem N°1.
Setting the problem
When one studies the formation of cristalline dendrites, one deals with a "free boundary problem".
There exists a family of solutions satisfying the transport equations in the bulk (thermal diffusion) and the equation of
the moving boundary (phase transition, surface tension). This solution is the family of parabolas due to Ivantsov.
In this family, each parabola moves formard, self-consistently, with a speed U, and the parabola is characterized by it radius of
curvature R.
Now, it is known that a singler parabola is observed, and not a family. It has been shown that the true aprabola is selected
by the anisotropy of the surface tension. The parabolas in the Ivantsoc family are not related in anyway to crystal structure. But the true
parabola grows with directions aligned with the crystal lattice. In efefct, the anisotropy of the crystal lattice selects
the observed parabola, among all the possible ones. But this parabola has a radius of curvature and a speed
U fixed by Ivantsov formula (more or less to some corrections).
This remarkable mathematical result was shown by Pelcé, Ben Jacob and others,
by introducing a perturbation of the form e.cos(m.teta) in the surface tension. e is a small quantity, m a wave number
and teta the polar angle in the real space. The selection problem was derived for m=4 and m=6.
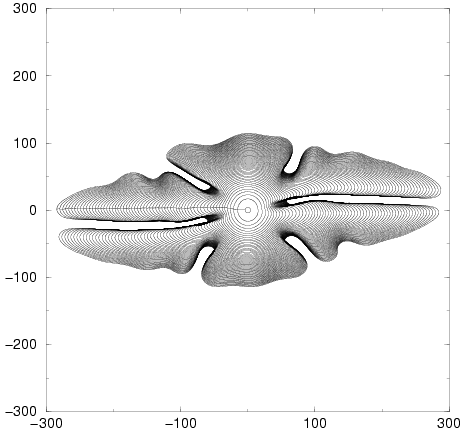
Here to the right, a crystal dendrite simulated by a phase field method.
(courtesy of Mathis Plapp).
|
 |
|
With Marcus Dejmek, we also adressed numerically the case m=2 which we would assume to correspond to an anistropy of fibers laid
along the surface. While working on that, I realized that the linear stability calculation was done for a sine-wave perturbation, although
there is no reason to do so. Any function may work. This is why I would like to re-do the calculation for a function
of the form
a+b(x)2 which would correspond to selection of the direction by a mere bump in surface tension.
A good start would be Pelcé's book on free boundary problems (Dynamics of cruved fronts, Ed. by P. Pelcé, Barnes and Nobles 1988, and also Théorie des formes de croissances, EDP Sciences).
|
 |
|
Problem number 2. Origin of writing.
Position of the problem.
The origin of writing may be in "fortune telling".
The chinese fortune tellers,4000 years ago, used to tell fortune with so called "oracle bones".
The predictions were done this way : turtle scales or bones were passed into fire. During rapid burning, the bony material would retract
and crack. The cracks were next interpreted, and sometimes over written to form meaningful patterns.
Hence, cracks produced by fire (under shrinkage, i.e. tensile stress) induced a meaning inside the brains of our ancestors. This means
that crack patterns are associated to a non random significance. Here to the right, some oracle bones found on the site of the University
of Hong Kong.
|


 |
|
The problem. If there is something in the brain which is so apt to read
ideograms, then there should be something particularly able to analyze and store the patterns in the brain.
But, these patterns seem to be crack patterns. Therefore, it should be possible to form a model of neural network (perceptron) able to
emulate the propagation of cracks.
In this case, the patterns of the ideograms would be stored in specific weak points of a cracking algorithm, and pattern recognition would
amount to actually "crack" a blank field of neuron states, by inducing some lateral neural-stress (a tensile stress).
More precisely, a 2D lattice of neurons should be able to emulate tensorial physics, by coding simply the synapitic coefficients
corresponding to a tensorial matrix of states.
By fixing some "fragility" spots, the crack pattern would be stored.
A starting point would be to code the lengths of sticks, as in the visual cortex, and to create a synaptic coefficient towards
lengths at right angles, in response to an outer stress, itself coded by an external stimulus.
|
 |
 |
|
Problem N° 3. Elasticity equations on a 3D shell.
I would like to use geodesic grids developped at Boulder, (for climate modelling) for elasticity problems on a sphere.
I had contacted the developpers and got the sources, but their is some work for a simulation expert
to code properly Hooke's law with this discretization scheme.
One can start by having a look at the site of the geodesic grids :
Le site des grilles geodesique.
Or by reading an article like :
a paper that explains it all.
|
 |
|
Problem N° 4. The self consistent 3D Wulff construction.
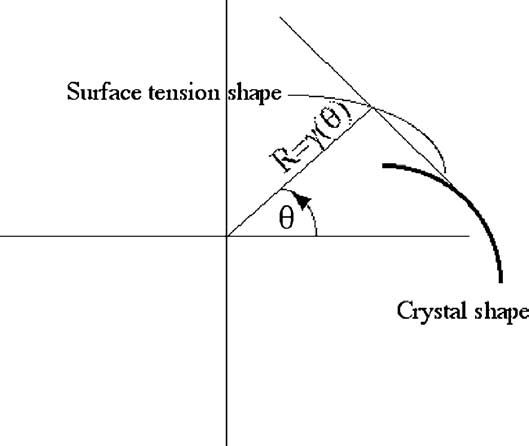
In order to caclulate the form of a surface that has non-even surface tension, one has to use the Wulff construction.
The Wulff construction is a mathematical trick that allows one to get directly the shape S(teta)
from the plot in polar coordinates
of the surface tension sigma(teta). The shape is the pedal of the surface tension. The pedal is the envelope of the normal
to the rays R(teta) where R(teta)=sigma(teta).
This comes from the fact that the surface tension minimizes the quantity Integral of [sigma.dl], and so does the pedal.
We may symbolize the tension force by little hands. When hands are bigger, the surface tension is higher.
If you think
of a circle of people holding each other by the hands, what would be the shape of the circle (indeed not circular)
if all people do not have the same strength in their hands.
The shape is obtained by forming the pedal of the function (strength of the hands).
The pedal is the envelope of the normal to the rays (strength), in polar coordinates.
This is the origin of facets and corners in crystals.
In the case of crystals, the strength is the atomic bond strength. This strength is not uniform, because it depends on
the orientation fo the atomic bond across the crystal lattice.
|
 |
|
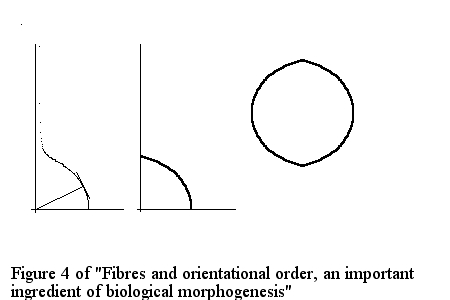
Problem N° 4. I have proposed to use Wulff construction in order to calculate the form of a fibred structure.
In this case one assumes that the surface tension depends on the drawing of the fibers in the surface.
For example, if fibers converge towards the poles, the surface gets stiffer. We then introduce an orientational vector n
such that sigma (the surface tension) varies as a function of, for example as div(n)2 (this is the K1 coefficient of Frank, for experts).
One then gets a surface profile having a "lemon shape".
I believe direction of growth of vegetal structures is selected by the anistropy,
(as proposed in Vincent Fleury and Tomoko Watanabe, About the equilibrium shape of fibred structures and biological shapes, C. R. Acad. Sci. série biologies, 327, 663-677 (2004).
with a few technical arguments).
/B> |
 |
|
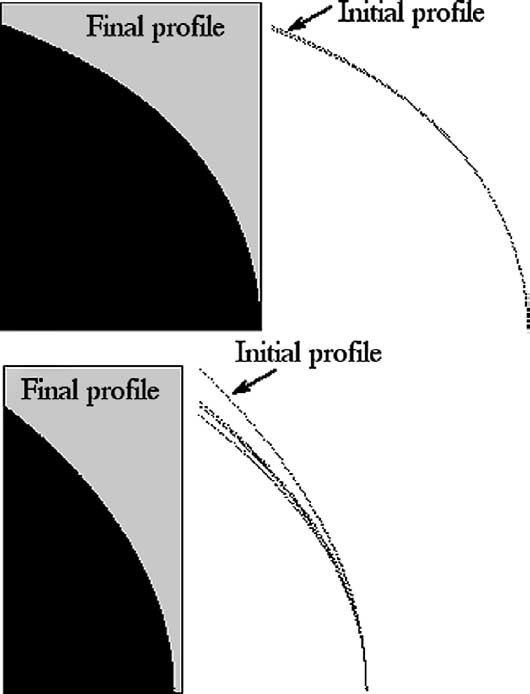
But now there is a problem, if the deformed surface is not spherical, one needs to recalculate
the pattern of fibers on the non-spherical shape (self-consistency of the equation).
I did it numerically in 2D for the wulff construction of convergent and meridian fibers.
In this case the surface satisfies simulatneously two conditions : it is the equilibrium shape of the fibers,
and the fibers follow tightly the surface which they generate.
This gives a somewhat blunt tip, as compared to the first order shape
(in which the divergence of the pole is not self-consistent
a sphere is assumed as shape, then div(n)2 is calculated, and then the shape is calculated from that,
although eventually, div(n)2 should
follow a different singular divergence towards the pole).
The shape is blunter because the divergence is less rapid on a lemon-like shape, as on a sphere (the pole is less flat).
|
 |
|
An undergrad student, Minh Binh Nguyen, made a few calculations of 3D shapes of crystals, whose surface tension is determined by
a drawing of fibers. He used the 3D Wulff construction, which is the envelope of the pedal planes.However, he did not do the same self-consistent shape, as the one I had done in 2D.
|
 |
|
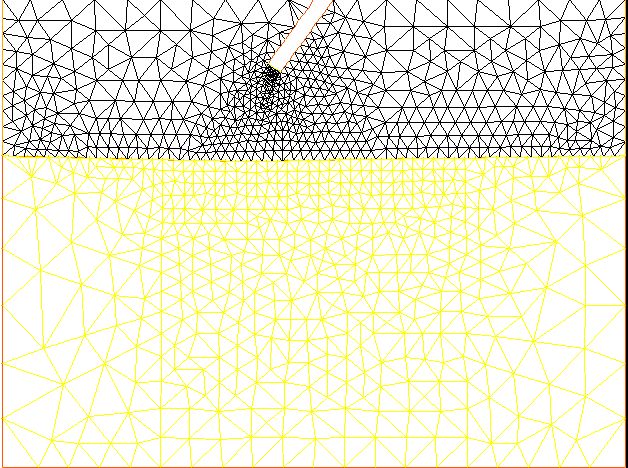
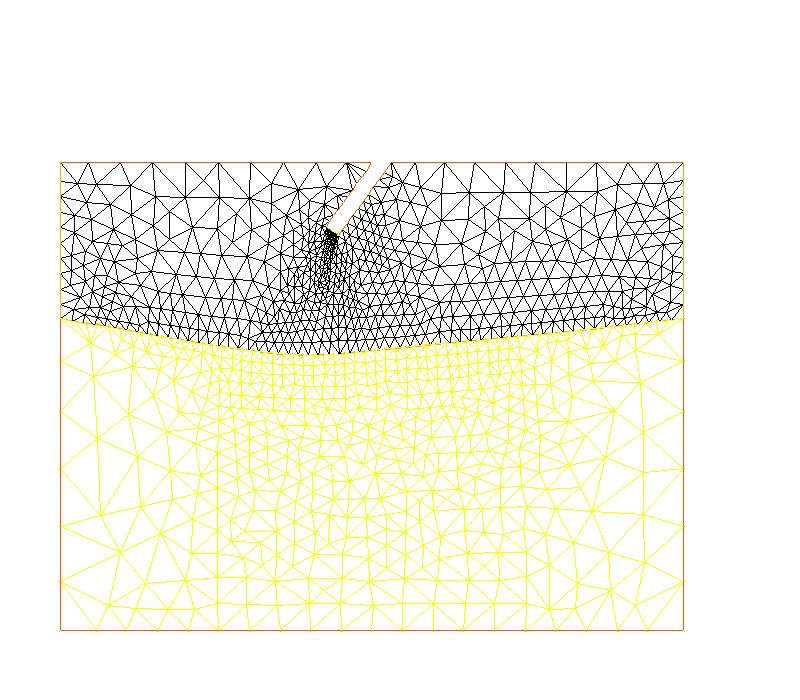
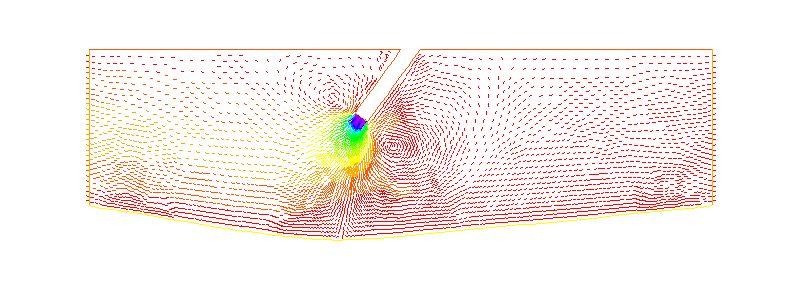
Problème N° 5. I have developped an instrument called "scanning air puff tonometer". This works by blowing an iar puff onto the surface of a given soft material.
I made a calculation of the air-surface interaction by finite elements (with Alia Al-Kilani).
I have used the Freefem++ code developepd by Hecht and Pironeau at the Inria.
Unfortunately I adressed only the 2D case. If you can help with a 3D solution you are welcome.
The calculation consists in doing a solution of deformation of a rectangular solid (Hooke's law) under the impinging air jet (solved with Navier-Stokes)..
|
|
|
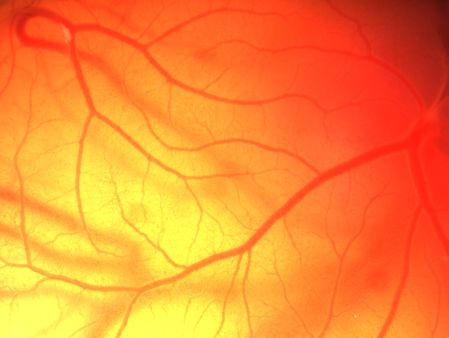
Problème N° 6. Physics of vascular branching
When one looks carefully at developping blood vessels, one realizes that, on the arterial side
and on the venous side, the intersections bend in the opposite way.
Here to the right, an image of blood vessels in the chorio-allantoic membrane (CAM), showing the main arteries.
The bifurcations are not sharp and straight.
They make an angle which is wider that one would expect.
(Photos VF. Membrane Chorio-allantoic of chicken embryos observed in "Shell less" culture,
by 5 days of development. Camera Scion corp couleur 12 bits, NIH Image for Scion Corp, binocular microscope Leica).
|
 |
|
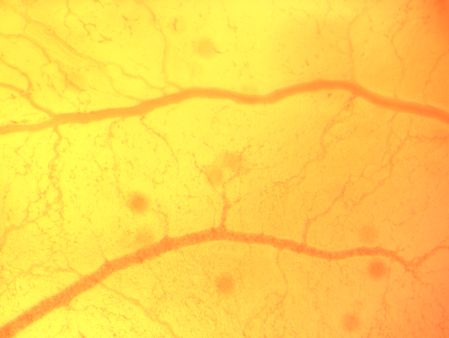
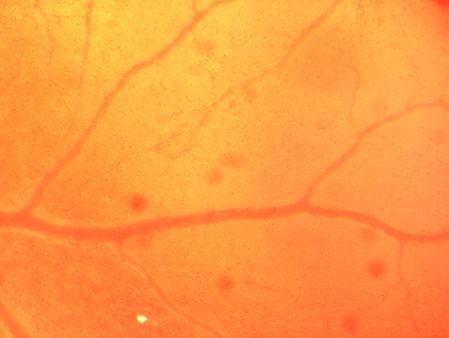
If we now increase the magnification, we zoom on tiny arteries and veins just being formed,we see that they too connect
to vessels which are higher in the hierarchy, by angles which have opposite mismatch with respect to a straight angle (the curvature
by which they connect has opposite sign). The equilibrium of the tubes would imply a straight 120) angle, or something like that. But there is a tangential
shear due to the flow, which has opposite value, on an artry as comapred to a vein, hence the result.
A cool measurement would be to plot the angle as a function of shear inside the tube (either directly by measuring the flows, or by taking
vessel diameter as a -non-linear- index of shear).
|
 |
|
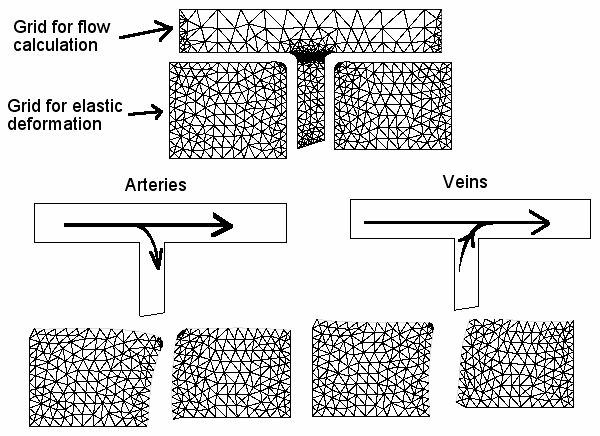
J'avais fait des calculs à 2D d'interaction fluide-structure (par éléments finis)
pour des bifurcations de capillaires sur le côté d'un gros vaisseau,
mais il faudrait refaire des calculs pour des formes plus générales,
avec des tuyaux 3D, posés dans un mésenchyme 2D. Par ailleurs,
il faudrait faire des expériences de suivi de la morphogenèse des vaisseaux (Time-lapse) pour
montrer que les vaisseaux se déforment dans le sens du cisaillement pariétal
(d'où les artères dans un sens, les veines dans l'autre).
Plus généralement, ces forces induisent des effets de couple (torque) dans
le tissu entre artères et veines, d'où une sorte de valse
(les paires de vaisseaux tendent à tourner corrélativement).
|
|
|
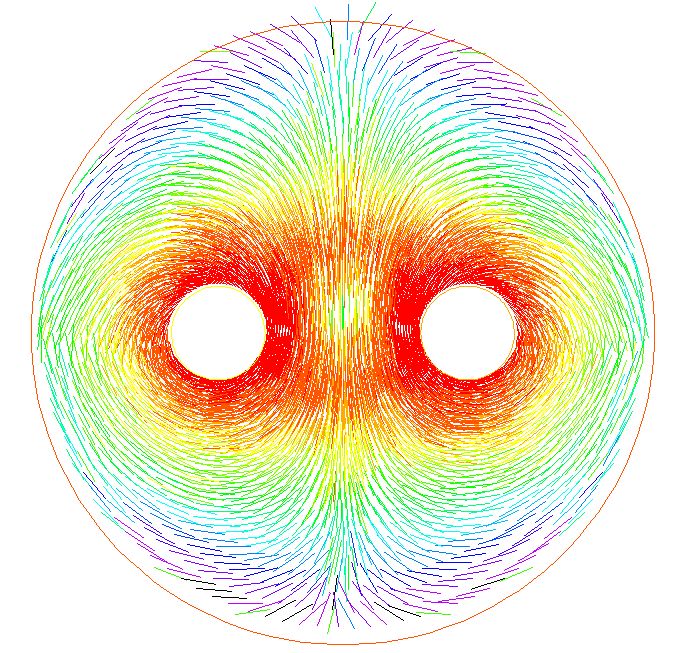
Problème N° 6: Le tourbillon visqueux auto-forcé.
Il existe en hydrodynamique quelques exemples bien connus de tourbillons. Comme par exemple la ligne de vortex.
Ces tourbillons sont en général inertiels, et, à 2D, peuvent s'ajouter les uns aux autres linéairement.
J'ai proposé récemment de modéliser la dynamique de formation des embryons par des tourbillons visqueux, entraînés par les cellules elles-mêmes.
Dans cette hypothèse, le problème à résoudre est de la forme nuLaplacien(V)-grad(P)=v/||v||.
C'est une équation non-linéaire. Dans ce type particulier d'hydrodynamique, c'est le fluide lui-même qui
se tire constamment "de l'intérieur". C'est un problème proche de la magnétohydrodynamique. ça a le mérite de fournir une équation fermée
modélisant la formation des animaux.
J'ai fait une résolution numérique par éléments finis,
mais je cherche la solution générale. La solution pour un tourbillon unique est un vortex auto-forcé
ayant un mouvement solide de révolution (très facile à montrer),
mais on ne peut pas superposer les solutions car le terme de source n'est pas linéaire.
Je cherche une solution générale pour N tourbillons.
|
|
|
La citation de la page :
|
"Si vous avez compris, vous avez sûrement tort", Jacques Lacan.
|
Publications.
Retour à la page de présentation-Back to front page RETOUR




















