I present here a few mathematical details about vortex flows
When a singular force acts on a fluid, the flow which is generated is called a "dipole".

A number of mathematical subtleties are linked to the dipole.

First, one should distinguish the kinetics, and the dynamics. This is to say : the velocities of the flow, and the forces which pull the flow. An incompressible fluid is characterized by the conservation law div(V)=0, which can actually be obtained with different forces. For example, in a tube div(V)=0 implies that the fluid speed is constant. That can be obtained either by pushing at one side, or pulling at the other side.

The image to the right shows the scalar values of Y(x,y), coded with a repeated grayscale (values modulo 256). Notice that the values on the upper half and lower half are inverted. This is normal since the vortices revolve in opposite direction, by symmetry.

The 2D flows V=(Vx,Vy), are constructed with a stream function.

Classical mathematics/physics of vector fields allows one to define a vector potential A which is perpendicular to the plane of the flow.

A=(0,0,Y(x,y)) such that the third component is a scalar satisfying V=curl((0,0,Y(x,y)).

The scalar function Y is called the stream function, and its iso-value curves are the streamlines.

This comes from the fact that the lines of grad(Y) and of curl(Y) are orthogonal. The figure to the right shows a few streamlines of a flow generated by a force located in the center (arrow).

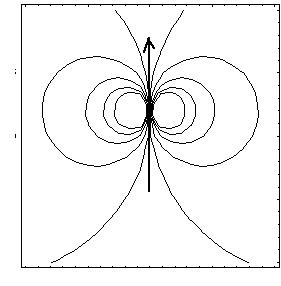
The mathematical formula for the dipole, in (x,y) coordinates, the axis Ox being along the force, and Oy being perpendicular to the force direction.

Note that the speed is infinite in the center. This is a "singularity", which is removed either physically by some other physics in that area (finite size effects, inertia terms, etc.) or mathematically by some "regularization", in terms of distribution functions.

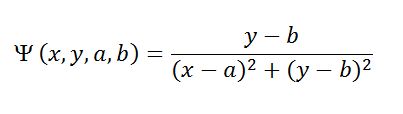
Once the formula for the dipole is known, one can integrate it over the distribution of such dipoles, in order to find the flow generated by this or that set of pulling forces. The integral of the force for forces oriented along Ox, but distributed along a segment oriented along Oy, is the sum of two logarithmic vortices.

Please note that the result of a uniform pull along a segment, is actually the sum of two vortices exerted at each end, a quite remarkable fact.

In this formula, -b and +b are the location of the center of the vortices along the axis Oy.
The corresponding streamlines.

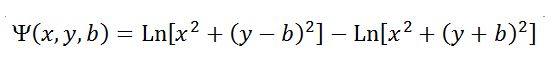
Please note that they form some sort of a funnel. By conservation law, the fluid accelerates in the funel. The difference with the single force pulling, is essentially that the funnel is wide (width 2b) therefore the singularity in the nip of the funnel is removed.

However, the flow is still singular in the core of the vortices.

Once the formula for the dipole is known, one can integrate it over the distribution of such dipoles, in order to find the flow generated by this or that set of pulling forces. The integral of the force for forces oriented along Ox, and distributed along a segment also oriented along Ox, is a trigonometric function.

Please note that it is actually the sum of two skewed monopoles located at each end of the line.

The virtue of this function is to elongate the vortices in proportion to the length of the segment
The corresponding streamlines.
Once the formula for the dipole is known, one can integrate it over the distribution of such dipoles, in order to find the flow generated by this or that set of pulling forces. The integral of the force for forces oriented along Ox, and distributed along a rectangle of boundaries fixed at x=-a, x=+a, y=-b, and y=+b can be obtained by integrating the trigonometric functions of the line of dipoles, between -b and b. This can be done exactly, and it gives the flow created by a patch of cells pulling themselves forward.

The corresponding streamlines.Remember that the inversion of colors across the Ox axis, is due to the change in flow direction (the vortices on either side revolve in opposite directions).
In all these examples, the force is static. This can be the case if the tissue is pulled by some pump, which is fixed at coordinates (a,b). It is however not the case if the force flows. In general terms, vortices flow with a speed equal to the speed imparted by the other vortices in the problem. This is a consequence of singular perturbation analysis. This consists in assuming that there are several identified vortices ("singularities"), and that the complex flow of the entire field can be reduced to the movements of their centers M each with speed u (M).

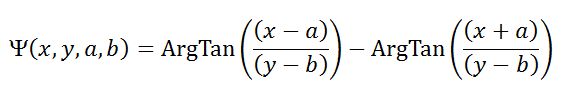
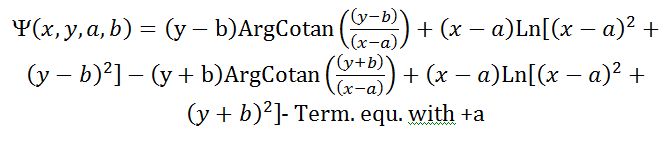
When implementing this into the Stokes equation, one finds a compatibility condition, which is that the speed u(M) for each center M, is the speed V(M), exerted at M, by the OTHER vortices.

Therefore, one generally finds moving vortices. Vortices are not stationary solutions of hydrodynamic equations.

A classical example is the vortex ring (smoke ring).

Adding a constant speed to a vortex flow is very easy in 2D, with the streamline formalism. A constant speed V oriented along X, corresponds to a scalar contribution Y(x,y)=Vy in the streamfunction (Please read, V multiplied by y, when the curl of (0,0,Vy) is taken, it drops a constant velocity V along Ox).

For the case of the wide patch of cells moving laterally, one finds easily the following pattern.

This I believe, is the explanation of limb bud formation, which has a lenticular shape, and of the navel formation (stagnation point).

La citation de la page : "Un savant, c'est quelqu'un qui sait des choses qu'il faudrait savoir mieux que lui pour être sûr que ce n'est pas un imbécile", Jean Paulhan.
End of page Back to animations of the course Retour à la page de présentation-Back to front page