Physics of vortices in embryos. Experimental evidence and models

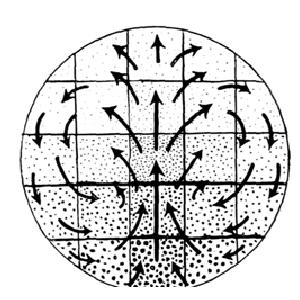
I am interested in the problem of vortex flows in embryo development. These vortices have been seen for a quite long time. But it is still difficult to model them properly. I am gathering here a number of experimental observations, and of theoretical insights. My own work follows a hydrodynamic approach. In particular, I have explained the emergence of a saddle-point in embryo development, which splits the movements into four domains of opposed chiralities. Most workers in this field quote Wetzel's work and especially this figure. Wetezl had already seen these vortices in 1924 -sorry 1929- (Wetzel R., Uber den primitivknotten des Hühnchens, Vehr. physik.-med. Ges. Würzburg 40, H.5 1929)
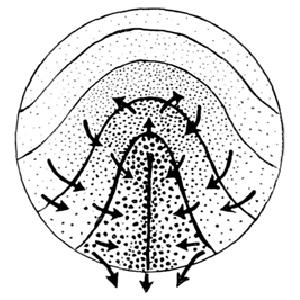
But most researchers neglect the next figure of Wetzel's work, which shows a posterior recirculation, which creates what we call a saddle-point.
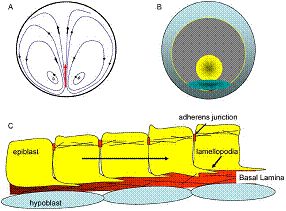
Recent articles show generally a pair of vortices, but do not build the dynamics around the saddle-point. For example in Weijer's group in Dundee, the dipolar field is modeled, but inside a static circle, while the blastula is actually a free boundary.
Weijer and co-workers do see a saddle point, by following the tissue field by PIV. The red square frames the saddle point which separates the field into four domains.
More recently Newman (in Multiscale modelling of developmental systems, Grid-Free models of Multicellular Systems, and application to large-scale vortices accompanying primitive streak formation 2007) builds a self-organized field of tissue displamcement associated to cell polarities. However there is no saddle point in this moddle, likely because of the boundary conditions. NB: in a completely hydrodynamic model, the initial polarity imposes itself to the vortices, these align the cells in the flow of V so that the cell polarity is evrywhere equal to V/||V||.
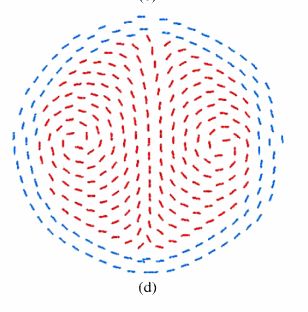
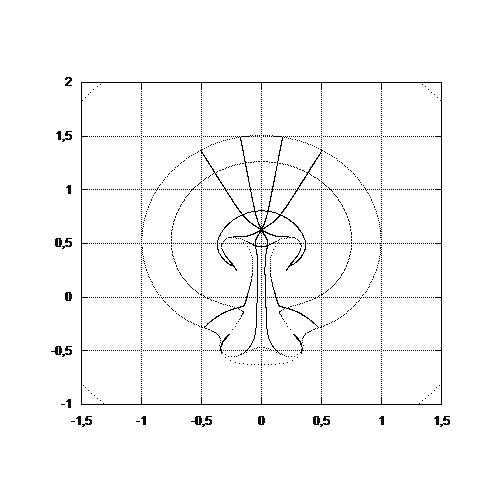
I have propsoed to treat the run away flow of the blastula as a hydrodynamic flow, launched by Kollerrauber's sickle. In an approximate mathematical form the flow will have the shape shown here. It implies a flatening of the flow towards and away from a saddle point. There exists a recirculation towards the posterior area which elongates the blastula posteriorily (in a "caudal" shape).
From : V. Fleury, La mathématisation complète d'un vertébré s'avère possible, Revue des questions scientifiques, 2007. This is the shape taken by a mosaic of cells, as it passes through a quadrupolar flow, composed of two dipoles oriented head-on. The animation can be viewed.
Continuation of the "vortex" presentation. See more vortices
The quotation of the page : "How well does he speak, he who speaks in the desert", André Gide.
Go back to front page