A few words about formation of blood vessels


|
A few words about formation of blood vessels |
|||
| I am interested in the formation of the blood vessels. I am particularly interested in understanding the mechanical or biomechanical features of their establishment. One question is how does flow, via shear stress and transmural pressure, progressively change their shape. Here to the right, this plate shows a blood vessel in the yolk-sac, seen from one end to the other. At one end, it is a lattice of capillaries, and one hardly distinguishes the vessel itself from the capillaries connected to it. It would be phsyically impossible to separate the evssel from the tissue. At the other end, it is a strong tube, completely disconnected from the tissue. Actually, all vessels, whatever their final size, were initially small capillaries, and formation of a true large tube is matter of progressive transformation of capillaries under, among other things, the action of mechanical forces. |  |
||
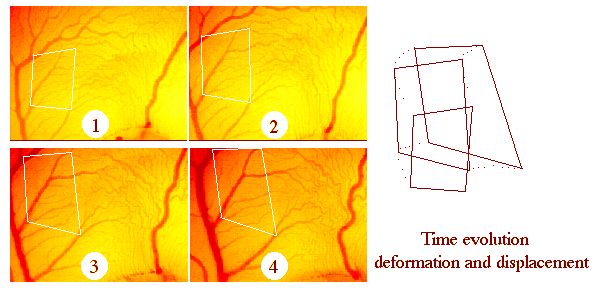
| I am also interested in forces around the vessels (not just the flow inside). The small incremental forces of the surrounding tissue add up to displace the tubes visco-elastically, more or less "like hoses". The plate to the right shows an example of measurement of displacements of vessels during time, during the development of the yolk-sac of the chicken. (The yolk-sac is an organ lying on top of the yolk, and surrounding the embryo, through which the embryo digests the yolk, it is similar to the placenta of the mammals, it is practical for optical imaging and for modelling, being the simpler of all organs). |  |
||
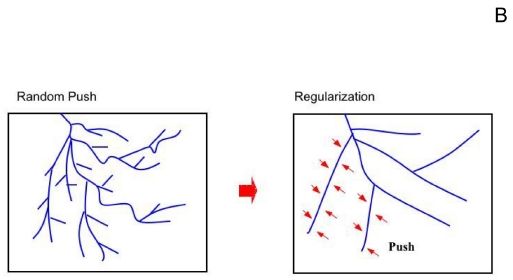
| An important point, worth understanding, is that there exists a a continuum deformation rate adding up small incremental displacements, so that, if one wants truly to understand morphogenesis, one needs to integrate, in the mathematical sense, the entire deformation rate field during time. The plate here to the right shows a scheme of the effect of the surrounding tissue. As the tissue pushes, because of growth, and migration, the vessels tend to resist (they have line tension), this induces a progressive "smoothing" effect. This transforms busshy vessels into more regular ones. |  |
||
| I have shown how one can explain the selection of a tree, inside a capillary bed, with dendritic growth models inspired from "river networks" models of self-organization (statistical models). I have extended these models to explain the "intertwinning" in 3D of the blood vessels. These ideas can be extrapolated to the case of the heart, viewed as an association of 4 large vessels. These models are based on the self-organizing properties of the viscous shear inside the tubes. These models are quite interesting in terms of both phylogeny and ontogeny, but they give somewhat unrealistic vessels (because they are stuck to a fixed lattice). This is true of most simulations in this field (never quite realistic). |  |
||
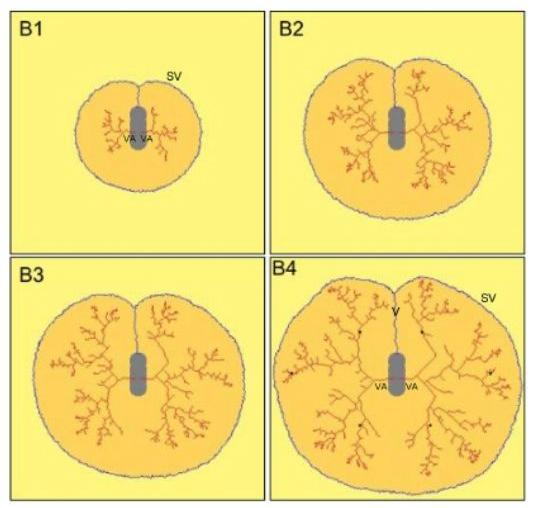
| In reality, as explained above, when vessels grow, so does the tissue around. During Thi-Hanh Nguyen's thesis work, we incorporated the effect of the surrounding tissue, which pushes continuously. We have used a Monte-Carlo method to model the self-organization of all vessels inside a yolk-sac. As far as I know, it is the only model that gives quite realistic vessels. What is absent in all the other models, is the slow effect of all small visco-elastic forces, which add up to deform and position the vessels. |  |
||
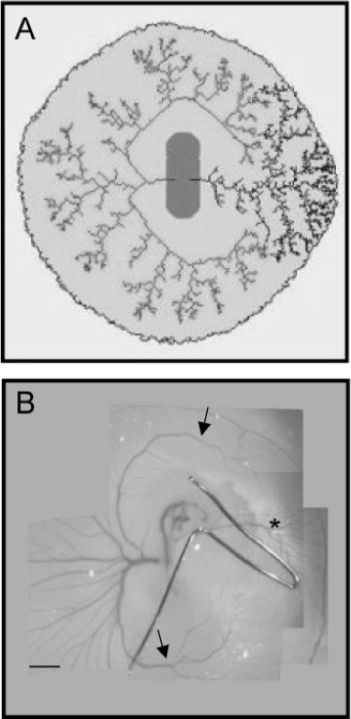
| Therefore, vessel morphogenesis is the sum of two physical phenomena (and many others, especially biochemical) : a fluid flow inside, and a slow creeping flow outside. One can next imagine experiments which either change the flows inside (occluding vessels for examples by clamping), or which modify the slow creeping flow around the vessels. The plate to the right shows an experiment of vessel clamping, and the corresponding simulation. The right vitelline artery is clamped by a small metal clip. That transforms the physiological quadrupolar flow into a dipolar flow, and an area in which an arterial tree should normally appear, sees the formation of a venous tree. |  |
||
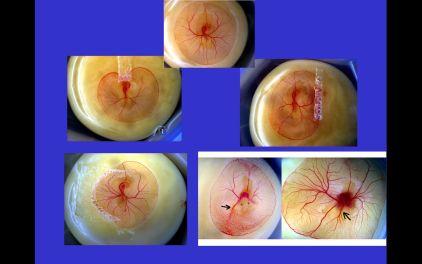
| The plate to the right shows a series of collision experiments, made with filter paper. The paper is welded onto the yolk surface and forms an obstacle to the yolk-sac expansion. The last case is that of twins, which share the same yolk This last instance may be important from the point of view of neonatal pediatry. . |  |
||
| Continue the blood vessels section The capillary regression | Retour à la page de présentation-Back to front page | ||
| The quotation of this page : | "The french cincema industry is just like everything else in France: not enough bucks." Michel Audiard. | ||