Deuxième partie de l'exposé présenté devant les professeurs de prépa.

Des progrès proprement extraordinaires ont été faits ces vingt dernières années dans la compréhension des formes de croissance, c'est-à-dire des formes obtenues par la déformation et l'évolution hors d'équilibre d'un contour ou d'une surface qui s'étend, s'accroît, augmente. Ces formes résultent d'une tendance de la surface à se lisser sous l'effet de la tension de surface (comme une membrane qui est tendue tend à devenir plus plate) d'une part, et d'autre part sous l'effet de l'accroissement de matière, qui est, lui, déstabilisant : là où arrive plus de matière, l'interface avance, puis elle tend à recevoir encore plus de matière etc. (sorte d'effet boule de neige, de croissance exponentielle). C'est le compromis des deux qui crée, au cours du temps, de façon dynamique, une forme, parfois extrêmement complexe, ou harmonieusement simple, selon le point de vue, comme les flocons de neige.

Mais revenons un peu sur la notion de forme d'équilibre.

La forme d'équilibre d'une surface, comme par exemple une bulle de savon, est le résultat de l'équilibre vectoriel, en tout point du contour, de la poussée interne de la pression, et de la force tangentielle qui accroche les molécules les unes aux autres.

Légende : Bulle de savon.

Chacun sait bien que le résultat est une sphère. C'est probablement l'origine de quelques formes sphériques dans la nature, ce qui a pu faire dire à Galilée que le livre de la nature était écrit en lettres de sphères (mais aussi de cones et de cubes).

Dans le cas de la sphère, la force d'accrochage des molécules, ou, si l'on préfère, l'énergie de surface (les deux sont porportionnelles) est uniforme; c'est pour cela que la sphère est une sphère.

Cependant dans bien des cas, cette force n'est pas uniforme. Si l'on songe aux cristaux, la force d'accrochage entre atomes ou molécules n'est pas uniforme, car elle dépend de l'environnement de chaque atome, et cet environnement varie le long de la surface, car le réseau cristallin fait en sorte que la distance interatomique dépende de l'orientation.

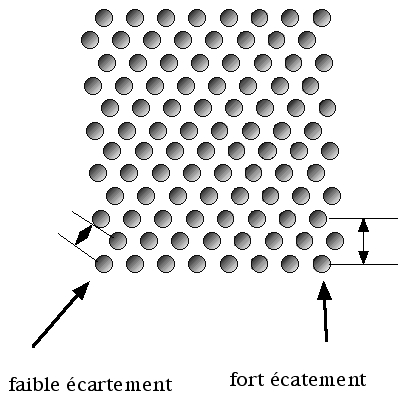
Légende. Distribution d'atomes dans un cristal.

Dans ce cas une force s'ajoute au contour, qui traduit la variation de la tension avec l'orientation. Le calcul de la forme d'équilibre n'est plus aussi simple, et il faut recourir à la construction de Wulff : la forme d'équilibre est la podaire de l'énergie de surface (ce point sera expliqué en détail lors de l'exposé). Pour obtenir la forme connaissant l'intensité en tout point de la force de traction entre deux voisins, il faut tracer la courbe donnant la liaison entre deux voisins (en polaire) puis tracer l'enveloppe des normales à cette courbe (c'est la podaire). Si la courbe est une constante (un cercle) la podaire est un cercle, c'est la bulle de savon. Si la courbe présente des maxima dans certaines directions cristallographiques, alors la forme est légèrement, voire très, "carrée". Ou bien même hexagonale, etc. cela dépendra du matériau considéé (quartz, diamant, sel de cuisine...). représentons l'intensité d'accrochage par de petites mains :

Légende. Energie de surface de la fonction R=constante, c'est un cercle, et la forme est circulaire.

Légende. Podaire de la fonction A+Ncos(4teta), on obtient une "bulle" assez carrée.

On voit donc que les propriétés de l'énergie de surface conditionnent la forme d'équilibre.

Il s'agit maintenant d'un problème de croissance dans lequel, d'une part, de la matière arrive sur la surface, qui tend à s'accroître dans la direction d'où vient la matière (plus y'en a, plus ça pousse), et qui d'autre part, essaie de trouver son équilibre à petite échelle en respectant la relation entre la courbure et le flux à l'interface. Au cas par cas, le problème peut dépendre précisément du type de champ choisi pour amener les nouveaux atomes à la surface. Champ diffusif (cas d'un gaz qui se solidifie), champ convecto-diffusif (croissance cristalline en présence d'écoulement), champ électrique (cas de la croissance électrochimique).

On observe alors le phénomène suivant. Si la tension de surface est isotrope, la forme se déstabilise et prend des allures de blobs de plus en plus compliqués.

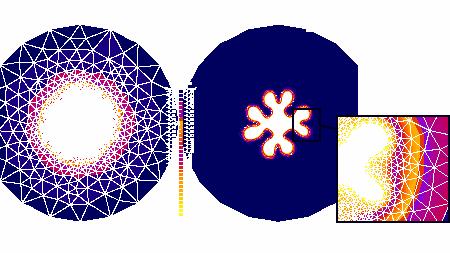
Légende. Croissance hors d'équilibre sans anisotropie de la tension de surface (Thèse de doctorat M. Dejmek).

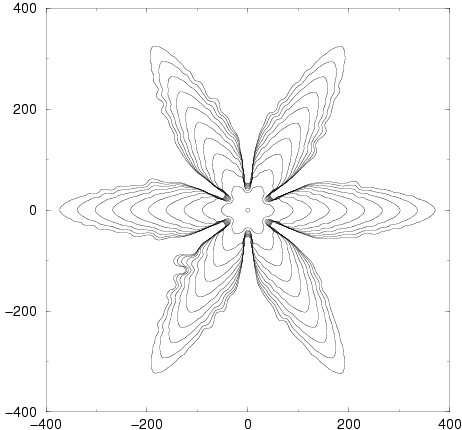
Légende. Croissance hors d'équilibre avec anisotropie de la tension de surface (ici anisotropie 6)Thèse de doctorat Marcus Dejmek.

Si la tension de surface est anisotrope, alors la forme se stabilise sur une forme plus régulière, dont la régularité s'appuie sur les directions privilégiées par la tension de surface. La démonstration de l'existence de ces solutions a demandé un travail très long, et une grande ingéniosité (perturbations singulières, théorie de la solvabilité).

Il existe également une autre forme plus curieuse : le doublon.

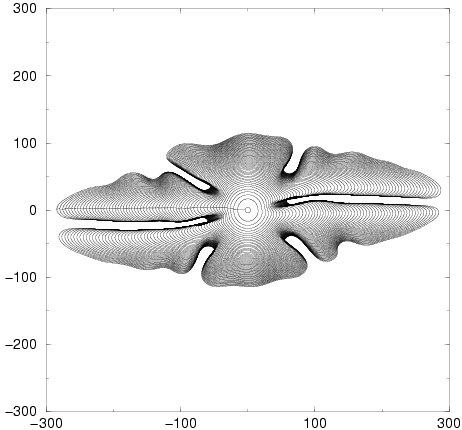
Légende. Croissance hors d'équilibre d'un doublon : une sorte de double pointe à symétrie miroir.

Ici, en gros, s'arrête le monde bien connu.

Cependant, rien n'impose que la tension de surface ait la forme A+Bcos(nteta) avec n=4 (sel de cuisine) ou 6 (flocon de neige). Et à vrai dire, rien n'impose qu'un matériau soit fait d'atomes alignés.

Regardons par exemple un navet ou un oignon. Cest une forme également non-sphérique, comme le cristal. Ces deux formes non-sphériques ont cependant un point commun : elles ont des bouts pointus. Ainsi, une extrémité du navet est pointue. C'est assez évident si on regarde le navet par la tranche, dans le sens vertical : il y a quelque chose comme un coin, au bout. On peut en dire autant des cristaux, ils sont un peu arrondis, parfois, avec des raccords de facettes en coins.

Légende. Navet, oignon. On remarquera l'existence d'un bout pointu.

Or ces structures, comme le navet, l'oignon, et nombre de formes biologiques analogues, sont faites non d'atomes, mais de cellules vivantes. Celles-ci ne se rangent pas sur un réseau cristallin, mais elles ont un ordre orientationnel, "nématique" ou nématoïde, un peu comme un cristal liquide.

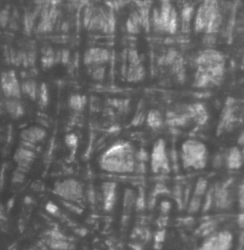
Légende. Ordonnancement de cellules à angle droits dans un navet.

Cet ordre induit des formes particulières de "gouttes" ou de "cristallites", présentant un ordre orientationnel, car l'énergie de la surface dépend de la façon dont les lignes sont dessinées, nouées, tricotées. Chacun sait qu'un tissu est plus ou moins dur, suivant que les mailles sont plus ou moins serrées. Ainsi, une même toile paraîtra plus dure ou plus molle suivant qu'elle est faite avec des fils plus ou moins serrés. C'est de cette façon-là que le tracé des filaments ou des alignements de cellules influe sur la forme.

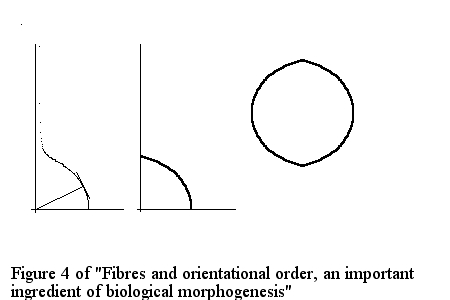
Imaginons une sphère qui serait fibrée comme "une balle de tennis". C'est une sphère ayant quatre pôles, si on appelle pôles les défauts topologiques d'alignement. Peut-on déduire la forme du "cristal" correspondant? On doit s'attendre à une forme ayant des singularités dans les régions des "pôles".

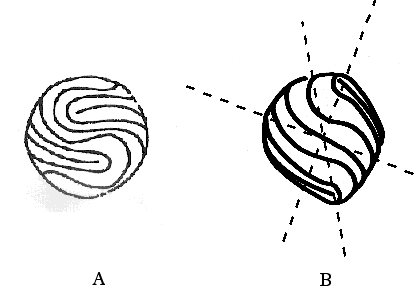
Légende. Balle de tennis, et forme correspondante.

Vous pouvez retrouver le détail de ce travail sur le site de Binh Minh Nguyen (élève étranger de l'Ecole Polytechnique en stage au laboratoire PMC).

Ce type d'idée s'applique à la forme des doigts, et plus généralement des organes fibrés, et même des plantes, comme nous allons le voir dans la partie suivante.

Troisième partie, la morphogenèse des structures fibrées.

Retour à la page précédente

Aller à la page suivante

Retour à la page de présentation