Gravity-capillary wave turbulence: Laboratory experiments 

For an overview: see our 2022 review in Annual Review of Fluid Mechanics.
We experimentally study gravity-capillary wave turbulence on the surface of a fluid to better understand the basic mechanisms of energy transfer between waves.

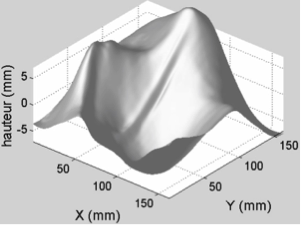
We have observed in laboratory the regime of gravity-capillary wave turbulence [1], and have reported the first experimental observation of intermittency in wave turbulence [2]. The intermittency is shown to not come from some coherent structures at large scale (wavebreakings, capillary bursts on steep gravity waves) [10,11]. Moreover, two major experimental challenges have been faced: the measurement of injected power [3], and of the wave field fully resolved in space and time [12]. At the time, those quantities were not yet been measured directly for wave turbulence on the surface of a fluid. Two main results have then been obtained: (i) Energy transfer mechanisms are not restricted to purely resonant wave interactions, as assumed by the theory, but involved other mechanisms related to the presence of strong nonlinear waves (sharp crested waves, bound waves, ...) [12]; (ii) The system shows large injected power fluctuations within the fluid [3], fluctuations not taken into account by weak turbulence theory. We showed that the distribution of injected power fluctuations is well described by a simple model [7]. A book chapter has been also published on the fluctuations in wave turbulence [19], as well as reviews on wave turbulence [6, 9].

We have then reported the first observation in laboratory of the direct gravity-capillary cascade when the fluid is not in a deep-water regime [14]. The study of nonstationary regime of capillary-wave turbulence, when the forcing is stopped, led to the first observation of decay wave turbulence [16]. Another optical method (different form Fourier Transform Profilometry used in [12]) called Diffusing Light Videography, has been used to reconstruct the capillary wave field both in time and space. We have highlighted the role of strongly nonlinear capillary waves on the turbulent dynamics [18, 30]. The study of 3-wave interactions between gravity-capillary waves allows us to validate experimentally, for the first time for noncolinear waves, the theory of 3-wave resonant interactions [24]. We have also obtain the first indirect measurement of the energy flux at each scale of the turbulent cascade [21]. As a consequence, the highlighting of dissipation at all scales of the capillary turbulent cascade (not taken into account in the current stage of theoretical developments) allowed to understand the disagreements observed, these last years, in numerous experiences on capillary wave turbulence. The constant of the Kolmogorov-Zakharov spectrum was also inferred experimentally for the first time and compared with its theoretical value [21, 23]. Besides, we performed the first direct numerical simulations of capillary wave turbulence from the two-phase Navier-Stokes equations [22]. These simulations confirm the validity of weak turbulence derivation when hypotheses are verified. Finally, we have studied for the first time wave turbulence on the interface between two immiscible fluids with free upper surface. We show that the coupling between free surface waves and interface waves modify strongly the wave turbulence regime [26]. We have also highlighted strong capillary-wave turbulence for which the interaction mechanism between waves becomes nonlocal and nonresonant (energy transfer through intermittent bursts) [30]. When viscous dissipation is significant, we demonstrated that the bandwidth of the free-surface transfer function is increased, allowing for three-wave interactions that do not satisfy the dispersion relation [33]. Finally, we reported the observation of nonlinear three-wave resonant interactions between two different branches of the dispersion relation of hydrodynamic waves, namely the gravity-capillary and sloshing modes [42]. Such a three-wave two-branch interaction mechanism is probably not restricted to hydrodynamics and could be of interest in other physical systems involving several propagation modes.

Gravity wave turbulence: Large-scale experiments 

Gravity wave turbulence is of paramount interest in oceanography but remains poorly understood [32]. Beyond observing the direct cascade of gravity wave turbulence, we showed in the laboratory that the gravity-wave spectrum is nonuniversal and depends on the forcing parameters [1]. We also reported the first laboratory observation of an inverse cascade of gravity-wave turbulence, but that was limited to a narrow inertial range due to the small-sized container used [15]. Moreover, we experimentally showed that a spatially homogeneous forcing leads to a good agreement with theoretical predictions [17], contrary to previous observations with a localized forcing with wavemakers.

We then conducted several measurement campaigns within a large-scale wave basin (50 m x 30 m x 5 m) at Ecole Centrale Nantes, France, to study gravity wave turbulence. The turbulent wave field is experimentally found to strongly depend on the basin boundary conditions (absorbing - beach or reflecting - wall) although their statistical and spectral properties are close [23]. We have also studied resonant interactions between nonlinear waves which are the fundamental mechanism that transfers energy in wave turbulence. The study of four-wave interactions between gravity waves allows us to validate experimentally, for the first time for noncolinear or perpendicular waves, the theory of four-wave resonant interactions [25]. For stronger nonlinearities, meaningful departures from this weakly nonlinear theory are observed [28]. Then, we reported the first experimental formation of the inverse cascade in gravity wave turbulence [36] stopped (not by finite-size effects as in [15]) by the emergence of nonlinear dissipative structures such as sharp-crested waves. We also showed that the presence of nonlinear coherent structures explains discrepancies from predictions of gravity-wave turbulence observed in oceanography and laboratory experiments [29].

By using the Large Diameter Centrifuge (LDC) of the European Space Agency, we were able to increase gravity by a factor of 1 to 20 times Earth's gravity to significantly extend the range of observable scales of gravity-wave turbulence in the laboratory. Moreover, the usual energy transfers (interaction between nonlinear waves) are found to be modified by the finite-size effects of the system [34].

We studied pure capillary waves in low-gravity environment during CNES Parabolic Flight Campaigns. We have observed pure capillary wave turbulence on a broad range of scales usually masked by the gravity wave regime on Earth [8]. Another advantage is to have a system with no boundary, the fluid covering all the internal surface of a spherical or cylindrical cell in low-gravity. Various patterns (hexagons, lines) have also been observed on a spherical fluid surface when the forcing is periodic [8].  See pictures of wave turbulence in space  ;  See also pictures of the team in Space

 This experiment of pure capillary wave turbulence was also performed for stronger forcing conditions onboard the International Space Station (ISS) in 2018 and 2021, in particular during CNES and ESA missions of the French astronaut Thomas Pesquet. The experiment called FLUIDICS (FLUId DynamICs in Space) was co-funded by CNES and Airbus. Strong wave turbulence is evidenced [31, 35].

  

Hydroelastic wave turbulence 

Hydroelastic wave turbulence focuses on random waves propagating on the surface of a fluid covered by an elastic sheet. It has been obtained for the first time in laboratory [20]. The existence of three-wave interactions, predicted theoretically in this system, has been highlighted experimentally [27].  

Hydroelastic waves, including gravity-bending waves, are found in various domains: on the surface of lakes or oceans covered by ice, or for very large floating structures in oceanography, flapping flags, or in biomedical applications such as heart valves. 

Quasi-1D wave turbulence

 Weak turbulence theory has been assessed experimentally in various wave systems propagating in two or three dimensions, but not in quasi-1D geometry since low-order resonant wave interactions are theoretically prohibited. We experimentally evidence, for the first time, quasi-1D capillary wave turbulence on the surface of a fluid in a canal. We also show that five-wave resonant interactions are the process generating such 1D capillary wave turbulence, which thus differs deeply from the 2D propagating case. We also report the first direct numerical simulation of quasi-1D capillary-wave turbulence [37]. 

Quasi-nondispersive wave turbulence

 We experimentally focused on the role of dispersion in wave turbulence, a subject that has received little attention although weak turbulence theory assumes wave dispersivity. Using a magnetic fluid in a canal, we experimentally reported a transition from dispersive wave turbulence to a non-dispersive regime dominated by random shock waves [41]. This is the first observation of a set of random shock waves on the surface of a fluid. We then demonstrated experimentally that this regime generates strong small-scale intermittency in agreement with a Burgerslike intermittency model, modified to account for the finite steepness of the experimental shock-wave fronts [43]. This intermittency is much more intense than the one previously reported in three-dimensional hydrodynamic turbulence or in wave turbulence. 

Magnetic wave turbulence and MHD

 We reported the first observation of a magnetic wave turbulence regime on the surface of a magnetic fluid submitted to a normal magnetic field [5]. To wit, we used a ferrofluid (a suspension of nanometric magnetic particles within a carrier liquid) for which its wave dispersion relation can be tuned by a magnetic field. The existence domains of gravity and capillary wave turbulence are also documented as well as a triple point of coexistence of these three regimes that are understood using dimensional analysis. Such an experimental system where the dispersion relation is tuned by the operator from a dispersive to a nondispersive system is thus of primary interest to test the wave turbulence theory (see above). The case of a magnetic field parallel to the fluid surface shows several differences with the normal case. The striking one is the meaningful broading of the inertial domain of the magnetic wave turbulence regime [13]. We have also carried out numerical work (three-dimensional direct numerical simulation) of free-surface magnetohydrodynamic wave turbulence, which demonstrates the existence of an analogy between anisotropic Alfvén wave turbulence in plasmas and wave turbulence on the surface of a magnetic fluid [40].

PUBLICATIONS on wave turbulence and wave interactions:

44. M. Vernet and E. Falcon 2025
     submitted to Physical Review Letters (2025)
     Thermodynamics and statistical equilibrium of large-scale hydroelastic wave turbulence

43. G. Ricard and E. Falcon 2023
     Physical Review E 108, 045106 (2023)
     Experimental evidence of random shock-wave intermittency

42. F. Novkoski, C.-T. Pham, and E. Falcon 2023
     Physical Review E 107, 045101 (2023)
     Evidence of experimental three-wave resonant interactions between two dispersion branches

41. G. Ricard and E. Falcon 2023
     Physical Review Fluids 8, 014804 (2023)
     Transition from wave turbulence to acousticlike shock wave regime

40. E. Kochurin, G. Ricard, N. Zubarev, and E. Falcon 2022   
     Physical Review E 105, L063101 (2022)
     Three-dimensional direct numerical simulation of free-surface magnetohydrodynamic wave turbulence

39. E. Falcon and N. Mordant 2022
      Annual Review of Fluid Mechanics 54, 1-25 (2022)
      Experiments in gravity-capillary wave turbulence

38. G. Ricard and E. Falcon 2021
      Europhysics Letters (EPL) 135, 64001 (2021)
      Experimental quasi-1D capillary-wave turbulence on the surface of a fluid

37. E. Kochurin, G. Ricard, N. Zubarev & E. Falcon 2020
      JETP Letters 112, 757 - 763 (2020)
      Numerical Simulation of Collinear Capillary-Wave Turbulence

36. E. Falcon, G. Michel, G. Prabhudesai, A. Cazaubiel, M. Berhanu, N. Mordant, S. Aumaître & F. Bonnefoy  2020
      Physical Review Letters 125, 134501 (2020)
      Saturation of the Inverse Cascade in Surface Gravity-Wave Turbulence

31. M. Berhanu, E. Falcon & S. Fauve 2018
        Report to COSPAR (World Committee for Space Research), 42th Scientific Assembly, 14-22 July 2018, Pasasena, USA, CNES Ed., p. 66 - 67 (2018)
        Wave turbulence in microgravity

30. M. Berhanu, E. Falcon & L. Deike 2018
       Journal of Fluid Mechanics 850, 803 (2018)
       Turbulence of capillary waves forced by steep gravity waves

29. G. Michel, B. Semin, A. Cazaubiel, F. Haudin, T. Humbert, S. Lepot, F. Bonnefoy, M. Berhanu & E. Falcon 2018
       Physical Review Fluids 3, 054801 (2018)
       Self-similar gravity wave spectra resulting from the modulation of bound waves

28. F. Bonnefoy, F. Haudin, G. Michel, B. Semin, T. Humbert, S. Aumaître, M. Berhanu & E. Falcon 2017
      La Houille Blanche 5, 56 (2017)
      Experimental observation of four-wave resonant interactions in a wave basin
 
27. L. Deike, M. Berhanu & E. Falcon 2017
       Physical Review Fluids 2, 064803  (2017)
       Experimental observation of hydroelastic three-wave interactions
 
26. B. Issenmann, C. Laroche & E. Falcon 2016
      EPL 116, 64005 (2016)     
      Wave turbulence in a two-layer fluid: coupling between free surface and interface waves

25. F. Bonnefoy, F. Haudin, G. Michel, B. Semin, T. Humbert, S. Aumaître, M. Berhanu & E. Falcon 2016
       Journal of Fluid Mechanics (Rapids) 805, R3 (2016)
       Observation of resonant interactions among surface gravity waves

24. F. Haudin, A. Cazaubiel, L. Deike, T. Jamin, E. Falcon and M. Berhanu 2016
       Physical Review E 93, 043110 (2016)
       Experimental study of three-wave interactions among capillary-gravity surface waves

23. L. Deike, B. Miquel, P. Gutiérrez, T. Jamin, B. Semin, M. Berhanu, E. Falcon & F. Bonnefoy 2015
       Journal of Fluid Mechanics 781, 196 (2015)
       Role of the basin boudary conditions in gravity wave turbulence

22. L. Deike, D. Fuster, M. Berhanu, E. Falcon 2014
       Physical Review Letters 112, 234501 (2014)
       Direct numerical simulations of capillary wave turbulence

21. L. Deike, M.Berhanu & E. Falcon 2014
      Energy flux measurement from the dissipated energy in capillary wave turbulence
      Physical Review E 89, 023003 (2014)

20. L. Deike, J.-C. Bacri & E. Falcon 2013
      Nonlinear waves on the surface of a fluid covered by an elastic sheet
      Journal of Fluid Mechanics 733, 394 (2013)

19. S. Aumaître, E. Falcon & S. Fauve 2013
      Fluctuations of the Energy Flux in Wave Turbulence
      Advances In Wave Turbulence (Ed. V. Shrira, S. Nazarenko, World Scientific, Chap. 2, pp. 53-72, 2013)      

18. M.Berhanu & E. Falcon 2013
      Space-time-resolved capillary wave turbulence
      Physical Review E 89, 033003 (2013)

17. B. Issenmann & E. Falcon 2013
      Gravity wave turbulence revealed by horizontal vibrations of the container
      Physical Review E 87, 011001(R) (2013)

16. L. Deike, M. Berhanu & E. Falcon 2012
      Decay of capillary wave turbulence
      Physical Review E 85, 066311 (2012)

15. L. Deike, C.Laroche & E. Falcon 2011
      Experimental study of the inverse cascade in gravity wave turbulence
      EPL 96, 34004 (2011)

14. E. Falcon & C.Laroche 2011
      Observation of depth-induced properties in wave turbulence on the surface of a fluid
      EPL 94, 34003 (2011)

13. S. Dorbolo & E. Falcon 2011                                                      
       Wave turbulence on the surface of a ferrofluid in a horizontal magnetic field
       Physical Review E 83, 046303 (2011)

12. E. Herbert, N. Mordant & E. Falcon 2010
      Observation of the nonlinear dispersion relation and spatial statistics of wave turbulence on the surface of a fluid
      Physical Review Letters 105, 144502 (2010)

11. E. Falcon, S. G. Roux & B. Audit 2010
      Revealing intermittency in experimental data with steep power spectra
       EPL 90, 50007 (2010)

10. E. Falcon, S. G. Roux & C. Laroche 2010
      On the origin of intermittency in wave turbulence
    EPL 90, 34005 (2010)

9. E. Falcon 2010
      Laboratory experiments on wave turbulence
      Discrete and Continuous Dynamical Systems - Series B Vol. 13, N°4, 819 - 840 (2010)

8. C. Falcón, E. Falcon, U. Bortolozzo & S. Fauve 2009
        Capillary wave turbulence on a spherical fluid surface in zero gravity
       EPL 86, 14002 (2009)

7. C. Falcón & E. Falcon 2009
       Fluctuations of energy flux in a simple dissipative out-of-equilibrium system
       Physical Review E 79, 041110 (2009)

6. E. Falcon  2008
       Etudes Expérimentales en Turbulence d'Ondes
       Habilitation à Diriger les Recherches, 244 pages, Université Paris Diderot (2008) (in french)
 
5. F. Boyer & E. Falcon 2008                                                        
        Wave turbulence on the surface of a ferrofluid in a magnetic field
       Physical Review Letters 101, 244502 (2008)

4. S. Fauve & E. Falcon 2008
        Gravity-capillary wave turbulence
       Report to COSPAR (World Committee for Space Research),  37th Scientific Assembly, 13-20 July 2008, Montréal, Canada, CNES Ed., p. 90 - 91 (2008)

3. E. Falcon, S. Aumaître, C. Falcón, C. Laroche & S. Fauve 2008
        Fluctuations of energy flux in wave turbulence
        Physical Review Letters 100, 064503 (2008)

2. E. Falcon, S. Fauve & C. Laroche 2007
          Observation of intermittency in wave turbulence,
          Physical Review Letters 98, 154501 (2007)

1. E. Falcon, C. Laroche & S. Fauve 2007
          Observation of gravity-capillary wave turbulence,
          Physical Review Letters 98, 094503 (2007)