granularmedia.html

Non Linear Physics Group - Eric Falcon

Granular Gases

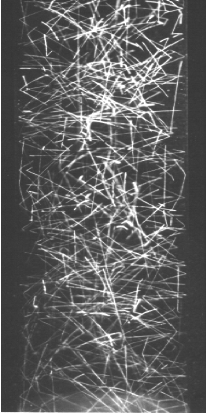
Due to inelastic collisions between particles, granular gases display striking properties compare to molecular gases such as cluster formation, and non-Gaussian velocity distribution.

Ground experiments:

- Spatially homogeneous forcing:

Most previous experimental studies on dissipative granular gases was performed by continuously vibrating a container wall to reach a non equilibrium steady state. Such a boundary-forcing is known to affect the granular gas properties. A spatially homogeneous forcing, driving each particles randomly, is thus needed to probe the validity domain of granular gas theories, but was hardly reachable experimentally so far. A new experimental technique is used to obtain a homogeneously driven granular gas in a three dimensional container. Such a spatially uniform and random forcing is reached by driven only rotational motions of particles.

Several major differences with respect to thermodynamiclike gas and boundary-forced dissipative granular gas: (i) the equation of state displays strong analogy with the usual gas one apart from a geometric factor (container-particle aspect ratio), (ii) the particle velocity distribution displays an exponential tail, and (iii) no cluster formation occurs even at higher density.

See movies in Equation of state of a granular gas homogeneously driven by particle rotations E. Falcon, J.-C. Bacri & C. Laroche EPL (Europhysics Letters) 103, 64004 (2013)

- Boundary forcing:

* Clustering formation, pressure and density measurements E. Falcon, S. Fauve & C. Laroche, European Physical Journal B, 9, 183-186 (1999)

* Experimental determination of a state equation for dissipative granular gases E. Falcon, C. Laroche & S. Fauve, Journal de Chimie Physique, 96, 1111-1116 (1999)

* An experimental study of a granular gas fluidized by vibration E. Falcon, C. Laroche & S. Fauve in "Granular Gases", Vol. 564 of Lectures Notes in Physics, T. Pöschel &S. Luding (Eds.), Springer, Berlin, p. 244-253 (2001)

Micro-gravity experiments:

* Collision statistics of a dilute granular gas in zero gravity. E. Falcon et al., Europhysics Letters 74, 830 (2006)

* Clustering formation in micro-gravity (see also here). E. Falcon et al., Physical Review Letters, 83, 440-444(1999)

(For an overview on experiments of granular media in low-gravity)

Numerical simulation:

Simulation of vibrated granular medium with impact - velocity - dependent - restitution coefficient

We performed two-dimensional numerical simulations of granular media strongly vibrated in order to reproduce the results of recent experiments realized in presence (Falcon and al, EPJB 99) or in the absence (Falcon and al, PRL 99) of gravity. We show that a model of coefficient of restitution dependent on the impact velocity between two grains is necessary so that the simulations are in agreement with the experiments. We measure the power-law exponents of the granular temperature, the collision frequency, the impulse and the pressure of the gas with the velocity of the vibrating piston. When the system evolves from a homogeneous gaseous state (low density of particles) towards a cluster one (high density), these exponents decrease continuously with the number of particles. In the absence of gravity, a loose cluster appears close to the wall opposite to the vibrating piston, and acts as a shock absorber for the fastest particles leading then to anormal exponents; whereas in the presence of gravity, the cluster bounces as an inelastic solid block. All these results differ in a significant way from the classic kinetic theory of inelastic hard sphere, as well as the previous numerical simulations based on a constant coefficient of restitution.

References:
S. McNamara & E. Falcon, Powder Technology 182, 232 (2008)

S. McNamara & E. Falcon, Physical Review E 71, 031302 (2005)
S. McNamara & E. Falcon, in “Granular Gas Dynamics”, Vol. 624, Lectures Notes in Physics, T. Pöschel & N. Brilliantov (Eds.), Springer, Berlin, p. 347-366 (2003)