Autoportance aérodynamique d’une corde tractée Hydrodynamique / interaction fluide-structure

avec Juliette Courson, Margaux Abello, Wladimir Toutain & Bruno Andreotti

dispositif experimental — Superposition de clichés d'une corde légère propulsée à différentes vitesses, vers le haut et la droite, par le système d'entraînement à gauche. Le changement de vitesse fait passer la corde d'une boucle pendante dominée par la gravité, à une forme en fuseau auto-portée grace au frottement de l'air.

La « corde charmée » fait partie de ces phénomènes impliquant un objet du quotidien, dans un montage qui tient sur un coin de table, dont l’explication s’avère plus subtile qu’il n’y paraît à première vue. Propulsez une corde nouée en boucle vers le haut, en l’entraînant par des poulies ou un jet d’air. À basse vitesse la corde vire immédiatement vers le bas, et suit la même forme pendante qu’elle adopte au repos. Augmentez la vitesse et vous constatez que les cordes légères se dressent alors, formant un fuseau allongé dans la direction de tir (cf. photo). On est tenté d’en conclure qu’il suffit de propulser la corde assez fortement pour qu’elle continue sur sa lancée tel un projectile, avant de rebrousser chemin pour boucler sur elle-même. Impossible cependant d’obtenir ces formes avec des cordes moins légères, alors que la même vitesse devrait les porter à la même hauteur au vu des expériences de Galilée, voire plus haut puisqu’elles sont moins freinées par le frottement de l’air. Une expérience sous une cloche à vide écarte définitivement l’hypothèse que la corde monterait par simple inertie: en retirant l’air même la corde légère retombe.

Cette observation fournit la clef de la solution: en analysant expérimentalement et théoriquement le rôle du frottement de l’air, nous avons montré que c’est bien lui qui soulève la boucle. C’est inattendu: le frottement, agissant dans le sens opposé au mouvement de la corde, est bien incapable d’engendrer lui-même une force de portance. Son intégrale le long de la corde bouclée s’annule en effet. Le couple engendré en revanche est non-nul, et provoque la rotation de la boucle autour du système de propulsion jusqu’à être compensé par un moment opposé du poids.

effective tension along string — Tension effective le long de la corde, en unités de son propre poids. À grande vitesse (noir, en m/s) la tension augmente le long de la corde à cause du frottement de l'air (rouge, normalisé). Le couple résultant soulève la boucle.

L’autoportance semble évoquer à première vue l’histoire du Baron de Münchhausen, qui se vante notamment de s’être extirpé, ainsi que son cheval, de sables mouvants en se soulevant par les cheveux. Il faut bien voir qu’ici la corde n’est pas isolée, puisqu’elle transmet, en l’entraînant, de la quantité de mouvement à l’air qui l’entoure. En faisant l’hypothèse d’un écoulement turbulent dans l’air, nous avons explicitement calculé le frottement résultant dans notre publication.

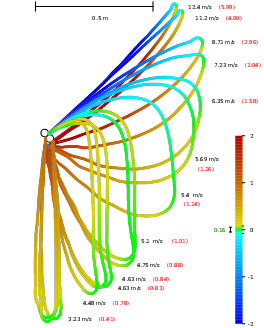
Le point le plus éloigné des poulies est un endroit critique, l’analogue d’un ressaut hydraulique dans un cours d’eau. Il marque le passage de la branche supérieure sur-critique — où les ondes transverses se propagent moins vite que la vitesse de la corde — à la branche inférieure sous-critique — où les ondes peuvent remonter à contre-sens. Une onde venant d’en bas ne pourra en revanche jamais franchir le point critique, elle ralentit de plus en plus à son approche.

space-time graph of transverse waves — Représentation spatio-temporelle (kymographe) de la propagation de perturbations (ondes) sur la corde. Le système de propulsion correspond au bord supérieur et inférieur, le point critique se situe au milieu (s-0). La corde va de haut en bas. On distingue bien le phénomène de ralentissement critique des ondes à l'approche du point critique.

La dynamique de la corde inextensible est complètement analogue à l’écoulement d’un fluide incompressible à une dimension, où la tension de la corde joue (avec un signe opposé) le rôle de la pression. Le point de rebroussement s’avère singulier dans les équations du mouvement: en première approximation la corde peut brusquement changer de direction. Expérimentalement on constate que la singularité est régularisée: le rayon de courbure ne s’annule pas vraiment.

Nous avons étudié ce système en préparant le French Physicists’ Tournament 2019, et en avons publié un compte-rendu dans le Journal of Fluid Mechanics. Deux autres compte-rendus ont paru de manière concommitante: l’un par les encadrants de l’équipe de l’ENS Lyon, un autre dans Emergent Scientist par une collaboration d’étudiants de différentes équipes FPT2019 dont la nôtre (Université Paris-Sud, ENS Ulm, Université de Paris).

On en parle…

La corde enchantée, un mystère élucidé (David Larousserie, Le Monde du 30 octobre 2019)
Étudier, experimenter, publier (Interview de Juliette Courson et de Margaux Abello; Service de communication, Université de Paris)

Last modified: 27 Jan 2022