Selbsttragende Seilschlingen durch Luftwiderstand Hydrodynamik / Fluid-Struktur-Kopplung

mit Juliette Courson, Margaux Abello, Wladimir Toutain & Bruno Andreotti

dispositif experimental
Eine leichte zur Schleife verknüpfte Schnur, durch gegenläufige Räder nach oben rechts gezogen, erhebt sich mit wachsender Geschwindigkeit von ihrer hängenden Konfiguration progressiv zu einer spindelförmigen Form.

Eine entlang ihrer selbst angetriebene Schleife aus leichter Schnur erhebt sich bei einer kritischen Geschwindigkeit in die Luft. Man könnte meinen die Schnur flöge hierbei einfach aus Trägheit in Schussrichtung (im Bild nach rechts-oben), und würde auf halbem Wege — da zur Schleife verknüpft — zur Umkehr gezwungen. Trägheit alleine reicht jedoch nicht, wie zwei Kontrollexperimente zeigen: erstens steigen schwerere Schnüre erst bei erheblich höheren Geschwindigkeiten nach oben, und zweitens bleibt auch die leichteste Schnur eine nach unten hängende Schlaufe, wenn man das Experiment in einem luftleeren Behälter durchführt.

Der Luftwiderstand ist folglich entscheidend. Der Wirkmechanismus ist interessant, denn zunächst scheint der Luftwiderstand überhaupt nicht imstande zu sein, die Schlaufe nach oben zu heben: der Nettoauftrieb, berechnet durch Summierung der lokal immer der Bewegung entgegengerichteten Widerstandskraft über die geschlossene Schleife, ist nämlich identisch Null. Das Drehmoment ist allerdings von Null verschieden. Es verursacht eine Drehung der Schleife um den Antrieb herum, bis es durch ein entgegengerichtetes Gewichtsmoment ausgeglichen wird.

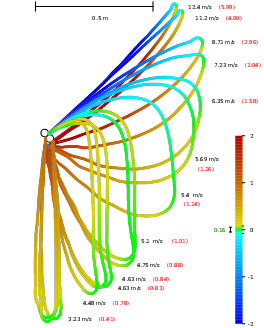
effective tension along string
Berechnete effektive Zugpannung entlang der Schnur, in Einheiten ihres Gewichts. Bei hohen Geschwindigkeiten (schwarz, in m/s) verursacht der Luftwiderstand (rot, normiert) einen monotonen Anstieg der Zugspannung entlang der Schnur. Das resultierende Drehmoment hebt die Schleife an.

Die selbsttragende Seilschlinge erinnert vielleicht auf den ersten Blick an den Baron Münchhausen, der sich und sein Pferd am eigenen Zopf aus dem Sumpf zieht. Im Gegensatz zu dieser Geschichte hat jedoch hier physikalisch alles seine Richtigkeit: die Schnur gibt Impuls an die umgebende Luft ab, indem sie letztere mitreißt. Unter der Annahme dass die Luft in der Umgebung der Schnur in turbulente Bewegung versetzt wird, haben wir den Luftwiderstand in unserer Publikation explizit berechnet.

Interessanterweise ist der vom Antrieb am weitesten entfernte Punkt (der Umkehrpunkt) ein kritischer Ort, analog zu einem Wechselsprung in fließendem Wasser: er markiert den Übergang vom oberen überkritischen (schießenden) Teil der Schlaufe, in dem sich transversale Wellen auf der Schnur langsamer bewegen als letztere, zum unteren unterkritischen (fließenden) Teil, in dem sich Wellen schneller ausbreiten — und sich dort mithin auch gegen die Bewegungsrichtung der Schnur fortpflanzen können. Kurz gesagt: Wellen können die Singularität stromaufwärts niemals überwinden. Sie können sich ihr nur nähern, wobei sie unendlich verlangsamen. Wie bei einem weissen (oder zeitumgekehrt schwarzen) Loch trennt ein Ereignishorizont den oberen vom unteren Teil der Schnur.

space-time graph of transverse waves
Raumzeitdarstellung (Kymograph) der Ausbreitung von Störungen (Wellen) entlang der Schur. Das Antriebssystem entspricht dem oberen und unteren Rand, der kritische Punkt befindet sich in der Mitte (s=0). Die Schnur bewegt sich von oben nach unten. Man sieht deutlich dass von unten kommende Wellen sich der Singularität nur nähern, sie aber nicht überwinden können.

Die Dynamik der Schnur ist formell vollkommen analog zum eindimensionalen Fluss einer inkompressiblen Flüssigkeit, in der die Zugspannung (mit umgekehrtem Vorzeichen) die Rolle des Drucks übernimmt. Der Umkehrpunkt der Schlaufe ist in den Bewegungsgleichungen singulär: in erster Näherung kann dort die Schnur in einem Knick diskontinuierlich die Bewegungsrichtung ändern. Im Experiment ist die Singularität jedoch nicht zu beobachten, Drücke und Schubspannungen durch die mitströmende Luft sowie elastische Momente begrenzen hier den Krümmungsradius.

Wir haben dieses System in der Vorbereitung des French Physicists’ Tournament 2019 untersucht, und unsere Funde im Journal of Fluid Mechanics publiziert. Zwei andere Publikationen sind ebenfalls nach dem Turnier erschienen, eine von den Team-Leadern der ENS Lyon, eine andere in Emergent Scientist aus einer Zusammenarbeit von Studenten dreier FPT2019 teams (darunter wieder unser Team — Université Paris-Sud, ENS Ulm, Université de Paris).

Erwähnungen an anderer Stelle…

Last modified: 18 Jul 2020