Exemples de programmes en C

Nous vous proposons ici quelques exemples de petits programmes en C. Ils ont un rapport variable avec le contenu des TD, mais illustrent divers aspects de la programmation. Ils vous proposent une solution particulière à un problème donné. Ce n'est jamais la seule, et pas forcément la meilleure. Nous avons juste essayé d'être court et clair en gardant le maximum de rigueur.

Si certains passage vous semblent obscurs:

Reprenez votre cours ou votre bouquin favori, et vérifiez la syntaxe. Vous allez probablement apprendre quelque chose.
Si la lumière n'a pas jailli, demandez à un(e) collègue.
Ensuite seulement, contactez nous par exemple par courriel ou lors du prochain cours. Il est très probable qu'il reste des erreurs. ...Mais nous avons fait beaucoup de tests :-)

Pour chaque programme, nous vous proposons le source (fich.c) et un jeu de données d'entrée (fich.in). Compilez le source avec la commande:

ordi:~ > gcc fich.c -lm -o fich

et exécutez en interactif par

ordi:~ > ./fich

ou en redirigeant l'entrée par

ordi:~ > ./fich < fich.in

Entrées/Sorties

Tout programme a besoin de données à traiter, et celles-ci varient généralement d'une fois sur l'autre. Les résultats doivent également être communiqués à l'utilisateur. Il est donc nécessaire de savoir lire et écrire des données en C. Ce n'est pas très difficile, mais il y a des pièges classiques. vous trouverez dans l'exemple proposé comment lire des données sur l'entrée standard (clavier) ou dans un fichier, et comment écrire les résultats sur la sortie standard (écran) ou dans un fichier, en l'occurrence le même. On vous montre également comment transmettre ces données entre le programme principale et des fonctions, par valeur ou par pointeur.

Tracé d'une fonction

Ce programme crée un fichier contenant deux colonnes (x, y) permettant de tracer la fonction de Gauss

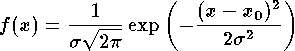
$f(x) = {1 \over \sigma\sqrt{2\pi}} \exp\left(-{(x-x_0)^2 \over 2\sigma^2}\right)$

Le fichier d'entrée contient la moyenne, l'écart type, le nombre de points à tracer et le pas. Ce programme illustre principalement les tests (if (...)) et la boucle for.

Recherche de zéro (L'échelle)

Ce programme recherche un zéro d'une fonction par la méthode de la dichotomie (sûre et lente). On y a particulièrement soigné les tests de vérification que les données proposées par l'utilisateur sont acceptables. C'est un des rare cas ou l'utilisation de goto se justifie.

Le problème "prétexte" est celui de l'échelle dans un couloir: Etant donné un angle droit entre deux couloirs de largeur a et b, quelle est la longueur de la plus grande échelle qui puisse prendre le virage?

Le coeur du programme est une boucle while controlée par un "flag". Les détails du test d'arrêt proprement dit sont renvoyés dans une fonction annexe.

Recherche de zéro - Newton

La métode de Newton-Raphson est beaucoup plus performante que la dichotomie, mais un peu plus délicate à utiliser. Le choix du point de départ est crucial.

Le programme proposé l'illustre sur le cas de la fonction atan(). Ici, aucune précaution particulière n'a été prise. Vous avez donc toutes les chances d'accumuler les ennuis si vous l'utilisez sans précautions. A vous de vous en inspirer pour écrire quelquechose de plus robuste...

Résolution d'équations différentielles

Il existe une pléthore d'algorithmes sophistiqués pour cette classe de problèmes, qui peut facilement remplir un un cours d'analyse numérique dédié. Le programme proposé se contente de comparer deux méthodes très élémentaires:

La méthode d'Euler (qu'il ne faut jamais utiliser).
La méthode d'Euler modifiée (bien meilleure à peu de frais)

Nous vous proposons trois équations différentielles ayant toutes trois des solutions analytiques, ce qui permet de comparer les solutions numériques et analytiques, et de calculer à chaque fois l'erreur relative.

On peut faire nettement mieux, mais c'est plus compliqué...

Auteur(s) : Anciens, A. Daerr. Dernière modification : Wed Nov 22 01:08:57 2006. [valid. XHTML]