Evaluation numérique de la dérivée d'une fonction
Méthode d'ordre 1
La façon la plus simple d'estimer la dérivée d'une fonction f continue, est d'utiliser la définition mathématique de celle-ci:
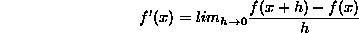
Graphiquement, on a l'interprétation usuelle de cette expression:
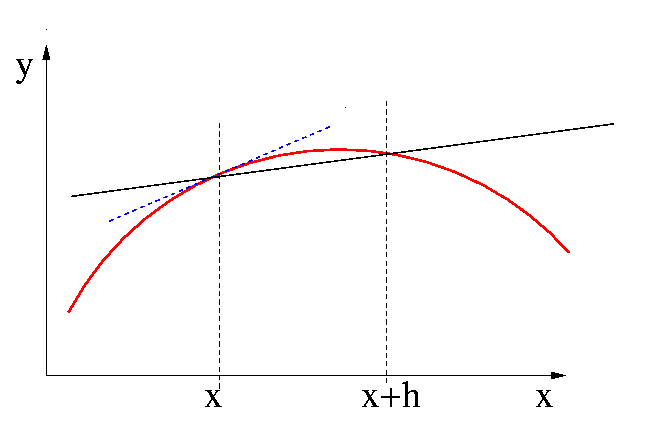
Pour obtenir l'erreur commise sur l'estimation, on peut faire un développement de f(x+h):
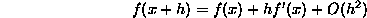
Ainsi, on a
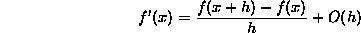
et l'erreur est d'ordre de h.
Cela pourrait paraître suffisant : il suffit de prendre h le plus petit possible. Mais numériquement, cela pose un problème: il faut calculer le rapport de deux nombres "petits" et les erreurs commises sont alors trop grandes. Cette méthode doit être évitée
Méthode d'ordre 2
Une méthode plus astucieuse est de "symétriser" l'expression de la dérivée. Graphiquement, cela revient à ne pas utiliser la valeur de f en x mais en deux points de part et d'autre (x-h et x+h).
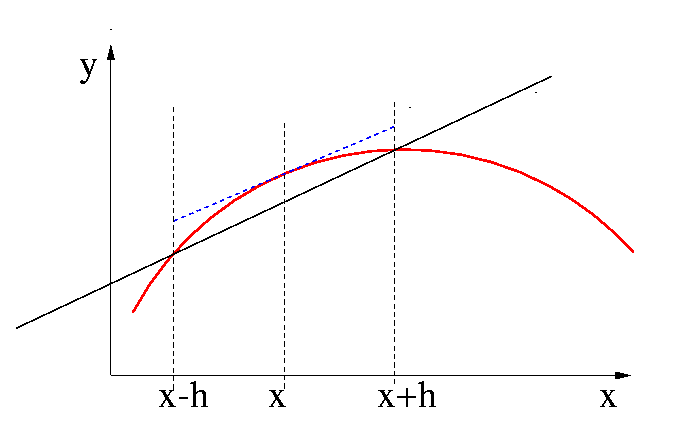
On voit alors que l'estimation est plus "proche" de la pente réelle en x.
La dérivée s'exprime sous la forme
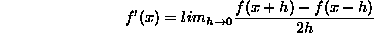
En développant f(x+h) et
f(x-h), et en prenant la différence,
le terme d'ordre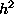 
disparaît:
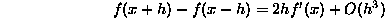
et
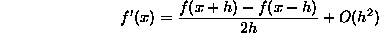
et l'erreur est d'ordr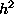e , ce
qui est bien meilleur pour peu de frais. Il faut donc
sytématiquement utiliser une méthode symétrique.