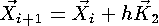Intégration d'équations différentielles y'=F(y,t)
Méthode d'Euler
On veut calculer numériquement, sur l'intervalle [t0,tn], la solution y(t) de l'équation différentielle:
dy/dt = f(y,t)
avec la condition initale
y(t0) = y0
Il nous faut donc connaître y(t) pour différentes valeurs t0, t1, ..., tn. La méthode d'Euler calcule yi+1 = y(ti+i) à partir de yi = y(ti) et de f(yi), sa dérivée à l'instant ti. C'est une méthode à un pas (h = ti+1- ti), ce pas pouvant être, éventuellement, variable.
L'algorithme de la méthode d'Euler consiste à faire un développement limité au premier ordre de y(ti+h) et à négliger le terme d'ordre h²:
y(ti+h) = y(ti) + hy'(ti) + O(h²)
soit
yi+1 = yi + hf(yi,ti)
Le principe est donc d'approximer la valeur de la fonction au pas suivant par la valeur prise par la droite tangente.
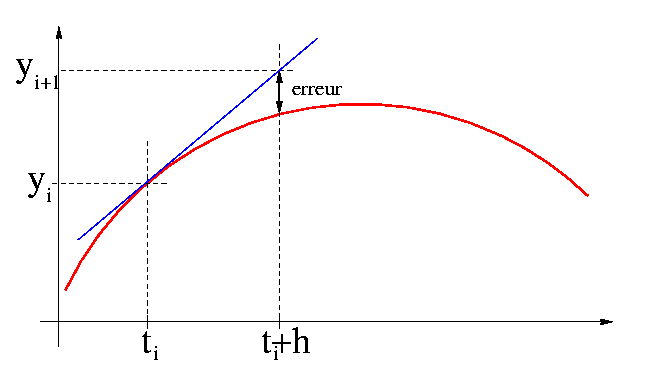
Cette méthode très simple est à déconseiller à cause de son manque de précision. Les méthodes d'ordres supérieur sont basées sur le même principe. Nous utiliserons la méthode d'Euler modifiée qui est d'ordre deux.
Méthode de Euler modifiée (ou méthode de Euler-Cauchy)
La modification aportée à la méthode d'Euler est similaire à celle utilisée pour calculer la dérivée d'une fonction, mais la problématique est ici inversée: on connait la dérivée (donnée par la fonction f) et on cherche le point de la courbe correspondant. L'idée est donc, au lieu d'utiliser la dérivée au temps ti pour trouver le point au temps ti+h, d'utiliser la dérivée au point milieu (ti + h/2).
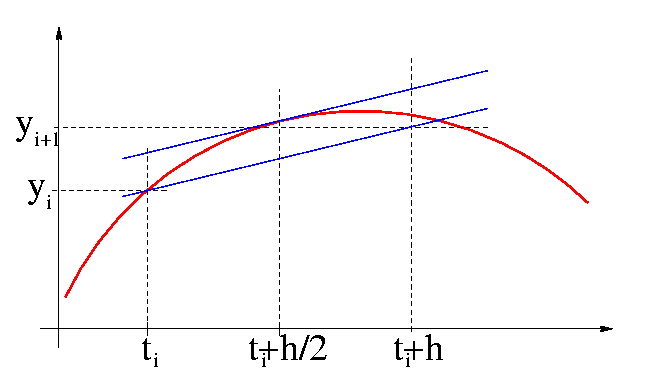
La dérivée en ce point est estimée par:
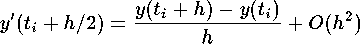
donc
y(ti+h) = y(ti) + hy'(ti+h/2) + O(h³)
On a de plus (y' = f(y,t)):
y'(ti+h/2) = f(y(ti+h/2), ti+h/2)
donc
y(ti+h) = y(ti) + hf(y(ti+h/2),ti+h/2) + O(h³)
Mais on ne connait pas y(ti+h/2), il faut donc l'estimer:
y(ti+h/2) = y(ti) + (h/2)y'(ti) + O(h²) = y(ti) + (h/2)f(y(ti),ti) + O(h²)
ce qui finalement donne l'estimation de la valeur au temps ti+1:
y(ti+1) = y(ti) + h f(y(ti) + h f(y(ti), ti)/2), ti+h/2) + O(h³)
On a donc bien gagné en précision (ordre deux au lieu de un).
Notons quand cette démonstration reste valable si f et y sont des vecteurs, et non de simple réels. Il n'y a pas de différence entre résoudre une équation différentielle, et un système d'équations différentielles.
Equations du second ordre
Dans le cas d'une équation du second ordre
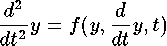
on se ramène à un système d'équations du premier ordre en introduisant une autre variable:
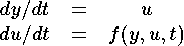
qu'on peut écrire sous forme vectorielle en posant
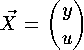
on a
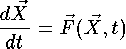
équation à laquelle on peut appliquer la méthode de façon tout à fait similaire. On a seulement augmenté d'une unité la dimension du problème en faisant baisser d'une unité son ordre.
Système d'équations différentielles
Dans le cas d'un système d'équations différentielles d'ordre quelconque, une manipulation similaire à la précédente (introduction de nouvelles variables) permet toujours de se ramener au cas d'un système (plus grand) d'équations du premier ordre, qui s'écrit également sous forme vectorielle
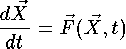
Un pas de la méthode d'Euler modifiée s'applique alors de la façon suivante:
- estimation de la valeur de la fonction après un demi-pas
(h/2)
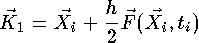
- Calcul de la dérivée en ce point
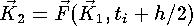
- Calcul du nouveau point