Hydrodynamics of wetting, capillary flows

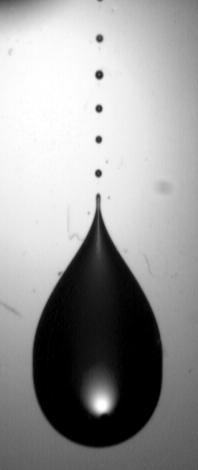
photo of sliding drops — Drops sliding down an incline change shape as a function of speed. Understanding the origin of the velocity threshold above which they leave behind a trail of small dropplets involves tackling the more general fundamental problem of wetting dynamics. Similar wetting transitions are observed in many industrial processes (printing, coating, ...), where a greater comprehension would be invaluable.

When a liquid has a free surface (with air above for instance), capillary forces (due to surface tension) come into play. These forces tend to reduce the free surface as much as possible, which is for example why a hole in a soap bubble or a thin liquid film will grow and destroy the latter. But in certain cases, which we study in our group, the flow of the liquid competes with the capillary forces and produces some unexpected behaviours:

drop Drops running down an inclined plane change shape, and form corners and cusps, which result from the great forces acting on their boundary.

meander Small rivulets meander on an inclined plane instead of flowing down along a straight path (like a single drop would do). It is not obvious why they do so.

photo of meandering rivulet — A small rivulet of water on an inclined plastic plane (here by 6°) does in general not flow down straight along the steepest slope. Why ?

The border of a drop or of a rivulet, the contact line, is a very singular place: not only do viscous forces tend to infinity in its vicinity, producing the dynamics just cited, but other quantities diverge as well:

wineStains In drying suspensions, the rate of solute concentration diverges near contact lines, so that particle deposition is inevitable. This leads to time-dependent pinning, and the formation of specific deposit patterns.

drop on parafin Drops deform soft substrates through capillary forces, which are localised near the contact line. This modifies the dynamics of spreading on gels.

As the thermal flux also diverges near a contact line, there is a competition between wetting and solidification when a liquid meniscus advances on a very cold substrate. This has obvious implications e.g. for ice formation on airplane wings in icy rain.

These examples of free surface flows, which are readily observed in everyday life (rain on a window, paint on a wall, stains from drying fluids, …) are representative of a number of flow configurations which pose practical problems in industrial processes such as printing, coating, food-processing etc. They also expose serious shortcomings in our present understanding of the fundamental physics of wetting, such as the incapacity to predict the speed of wetting.

hydrophobic leaf

Last modified: 18 Jul 2020