Étude du tube à choc

Équation aux dérivées partielles hyperbolique, problème de Riemann et discontinuités

Le système physique

L'un des dispositifs les plus simples pour étudier des écoulements supersoniques est le tube à choc: il s'agit d'un tube séparé en deux parties par une membrane. D'un coté (disons à gauche) le tube moteur, à pression pL élevée, et de l'autre coté le tube de travail, à pression pR plus basse. Lorsqu'à l'instant t=0 le diaphragme est rompu, les pressions tentent à s'égaliser: une onde de compression se propage dans le tube de travail (dans lequel se trouve éventuellement une maquette d'avion), tandis qu'une onde de détente remonte dans le tube moteur. Ces fronts sont plus ou moins abrupts et correspondent à des discontinuités de certaines grandeurs physiques (pression p(x), masse volumique ρ(x), température T(x) ou vitesse U(x)). Nous allons nous intéresser à la capacité de différents schémas numériques à décrire correctement l'évolution du système.

Conditions initiales et aux bords

Initialement, le gaz est au repos des deux cotés de la membrane (UL = UR = 0), et les autres grandeurs constantes dans le tube moteur (ρ(x,t=0) = ρL, p(x,t=0) = pL, T(x,t=0) = TL, ...) et le tube de travail (ρ(x,t=0) = ρR, p(x,t=0) = pR, T(x,t=0) = TR, ...).

À t = 0 le diaphragme disparaît abruptement. On s'intéressera au système surtout avant que les ondes de choc n'atteignent les bords du tube. Nous prenons donc la condition aux bords la plus simple qui vient à l'esprit: on maintient sur les bords la condition initiale (ρL, pL, TL, ... au bord gauche; ρR, pR, TR, ... au bord droite).

Les équations d'évolution

L'écoulement de gaz à l'intérieur du tube, si on suppose le gaz parfait et l'écoulement monodimensionnel, est décrit par le système d'équations d'Euler suivant: 

ρt + (ρU)x = 0
(ρU)t + (ρU² + p)x = 0
Et + ([E + p]U)x = 0

où les indices t et x symbolisent les dérivées partielles temporelle et spatiale, ρ est la masse volumique, U la vitesse, p la pression et E l'énergie totale 

p = ρRT
E = p/(γ - 1) + ρU²/2

(R et γ sont deux constantes caractérisant le gaz parfait). On a négligé les processus de diffusion moléculaire.

Équations sans dimensions

On peut adimensionner la vitesse par la vitesse du son dans le tube de travail, et les autres grandeurs de manière similaire par rapport à leur valeur initiale dans le tube de travail: U = a* U*, ρ = ρR ρ*, T = γTR T*, p = γpR p*, E = ρRaR² E*. En oubliant les *, on retrouve les mêmes équations d'évolution pour les grandeurs sans dimension: 

ρt + (ρU)x = 0
(ρU)t + (ρU² + p)x = 0
Et + ([E + p]U)x = 0
p = ρT
E = p/(γ - 1) + ρU²/2

tandis que la condition initiale devient 

Partie R: ρR = 1,  pR = 1/γ,  TR = 1/γ,  UR = 0
Partie L: ρL = ...,  pL = ...,  TL = ...,  UL = 0

Intégration numérique

Si on regroupe en un vecteur les quantités à déterminer: W = (ρ, ρU, E), on voit qu'on a une équation du type Wt + f(W)x = 0. En discrétisant le temps et l'espace: 

xj = j δx,   δx = 1/(Nx - 1), j = 0,...,Nx-1
tn = n δt,   δt = 1/(Nt - 1), n = 0,...,Nt-1

on peut donc appliquer un schéma d'Euler (où Runge-Kutta, Euler modifié, ...) en temps et un schéma de différences finies en espace. Considérons deux schémas explicites, MacCormack et Lax-Wendroff, dans lesquels la solution numérique Wjn+1 au pas de temps suivant est calculée en deux étapes (prédicteur/correcteur): 

Lax-Wendroff:
1) Zj+1/2 = (Wjn + Wj+1n)/2 - (δt/2δx)[F(Wj+1n) - F(Wjn)]
2) Wjn+1 = Wjn - (δt/δx)[F(Zj+1/2) - F(Zj-1/2)]

MacCormack:
1) Zj = Wjn - (δt/δx)[F(Wj+1n) - F(Wjn)]
2) Wjn+1 = (Wjn + Zj)/2 - (δt/2δx)[F(Zj) - F(Zj-1)]

Solution exacte

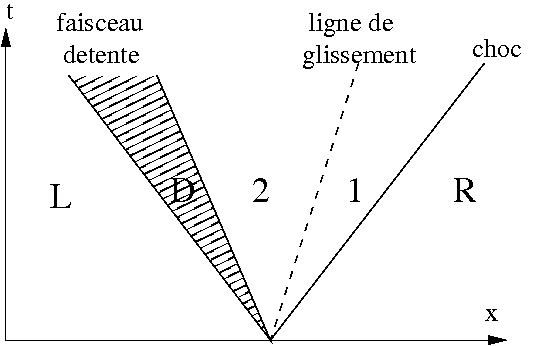
L'évolution de la masse volumique, de la vitesse et de la pression le long du tube à choc peut être calculée analytiquement. Vu qu'il s'agit juste de comparer cette solution exacte au résultats numériques, cette solution est donnée sans explications:

diagramme spatio-temporel du tube

  1. Les frontières des zones sont données par les abcisses suivantes:

    xLD = x0 - aL t
xD2 = x0 + (U2 - a2) t
x21 = x0 + U2 t
x1R = x0 + MS t

    où x0 est la position de la membrane, aL et a2 les vitesse du son dans les zones correspondantes et MS est le Mach de l'onde de choc.

  2. Les données du problème sont les paramètres sans dimensions des zones initiales R et L:

    Partie R: ρR = 1, pR = 1/γ, TR = 1/γ, UR = 0
Partie L: ρL, pL, TL, UL = 0

  3. Le passage de la zone R à la zone 1 se fait par une onde de choc instationnaire, de vitesse constante. Il faut déterminer le nombre de Mach du choc (MS = US/aR, où aR = sqrt(γTR) est la vitesse du son dans la zone R), solution de l'équation suivante (appelée relation de compatibilité):

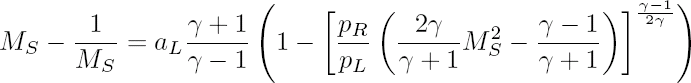
    relation compatibilité

  4. Les paramètres de la zone 1 sont constants et donnés par les relations de saut de Rankine-Hugoniot à travers le choc:

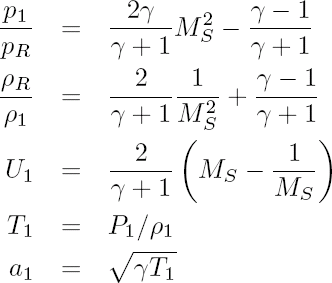
    relations Rankine_Hugoniot

  5. Le passage à travers la ligne de glissement est caractérisée par une discontinuité de masse volumique seulement, la vitesse et la pression étant conservées. Par conséquent: 
    U2 = U1, p2 = p1,
  6. Les paramètres de la zone 2 peuvent être reliés aux paramètres de la zone L en utilisant les caractéristiques de l'équation d'évolution. On obtient 
    ρ2 = ρL (ρ2ρL)1/γ,
a2 = aL - (γ-1)U2/2
Auteur(s) : A. Daerr. Dernière modification : Tue Nov 21 00:51:12 2006. [validate XHTML]