Minimisation: points de Lagrange d'un système à 3 corps

Nous allons étudier les états d'équilibre stationnaires d'une petite masse en interactions avec deux masses plus grandes. Il peut par exemple s'agir d'un satellite entre la terre et la lune, ou bien d'un astéroïde dans notre système planétaire, qui ressentirait surtout les deux corps les plus grands, à savoir le soleil et Jupiter.
On supposera qu'il y a une hiérarchie des masses (mSoleil >> mJupiter >>> masteroide), de telle façon à ce qu'on puisse négliger l'influence de l'asteroide sur les deux autres corps, et que le rapport μ = mJupiter/mSoleil soit petit.
Si on se place dans un référentiel tournant de manière à ce que le soleil et Jupiter se trouvent sur l'axe Ox (avec le soleil en x=-μ et Jupiter en x=1, le barycentre est à l'origine), on peut montrer que la quantité J = V²/2 + U est constante (appelée constante de Jacobi), où V est la vitesse de l'asteroide et U un potentiel qui dépend de sa position:
U = -(x²+y²)/2 - μ/r2 - (1-μ)/r1 + U0 avec U0 = 3/2 + (9/2)h² - 7 h³ + o(h4), h = (μ/3)^(1/3)
Ici r1 est la distance astéroïde-soleil, r2 la distance astéroïde-Jupiter. En particulier, les minima de cette fonction sont des points d'équilibre (en fait les maximas le sont aussi...), et c'est eux qu'on voudrait trouver.
- Écrivez un programme qui affiche la valeur de U(x,y) en un point
donné. Vérifiez le résultat en quelques points choisis (ou créez une
image au format pgm (c.f.
man pgm)). Pour le couple Jupiter/Soleil, μ=0.001 est une bonne valeur. - Utilisez une des méthodes proposée dans le cours (voir les notes) pour trouver les minima de U(x,y). Pour commencer, nous proposons par exemple d'utiliser la minimisation selon les directions cardinales (donc en alternant selon Ox et Oy).
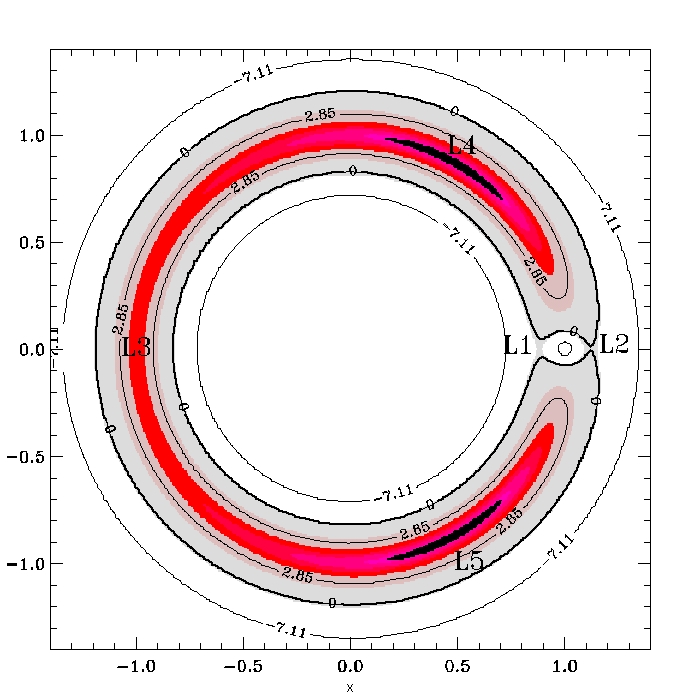
Pour vous guider, voici une image des iso-valeurs de U(x,y):