• Accueil
• TD 1: gnuplot, C, dichotomie
• TD 2: Euler (modifié) [pendule]
• TD 3: Euler implicite [pendule]
• TD 4: Runge-Kutta 4 [Bruxellateur]
• TD 5: EDP parabol [Chaleur]
• TD 6: EDP hyperbol [Tube à choc]
• TD 7: Equ linéaires [Polymère]
• TD 8: Nbres aléat., Monte-Carlo
• TD 9: Minimisation [points Lagrange]

• Documentation
• Unix
• C
• C++
• Java
• Python
• Comparatif langages
• Gnuplot
• Méthodes num.

• Nouvelles
• Notes de cours
• Enseignants

Prendre en main Linux, C, et gnuplot; résoudre f(x)=0 par dichotomie

Le but de ce TD est de vous faire connaître les outils dont nous aurons besoins tout au long du semestre:

• Linux, le shell
• un éditeur de texte
• le compilateur C: gcc
• un afficheur: gnuplot

et de vous faire résoudre un premier problème physique à l'aide d'un programme en C. Ce sera l'occasion de voir la méthode de la dichotomie pour trouver la solution d'une équation f(x)=0.

Le problème

Une cabine téléphérique chargée va pendre plus bas que lorsqu'elle est vide. Connaissant les propriétés charactéristiques des cables, peut-on calculer la position d'équilibre de la cabine en fonction de son poids ?

Problème totalement différent: Un constructeur de sommiers à ressorts veut savoir quelle raideur choisir pour ses ressorts pour qu'une personne pesant 100kg ne s'enfonce pas plus qu'une dizaine de cm dans le lit. On suppose que le lit fait 100cm de large et que la personne répartie son poids sur 20 ressorts tendus horizontalement d'un bout du cadre à l'autre.

On modélisera ces deux systèmes en ne gardant que les éléments suivants: une masse accrochée au milieu d'une corde élastique accrochée aux deux bouts:

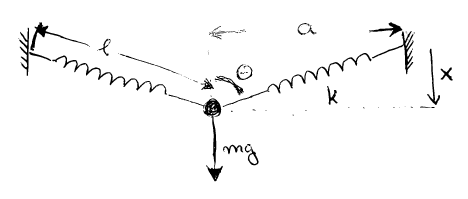
Pas à pas

• Écrivez la condition d'équilibre de la masse. On supposera que la longueur des deux ressorts est la même, et que leur longueur à vide vaut a.
• En remplacant x par ay, montrez qu'il ne reste plus qu'un paramètre sans dimension G=mg/ka dans l'équation.
• En prenant f(x)=G-2*x*(1-1/sqrt(1+x²)), trouver la position d'équilibre revient donc à trouver une solution à l'équation f(x) = 0. Est-il possible de la calculer explicitement ?
• Utilisez gnuplot pour afficher la courbe (pour G=0.01 par exemple). Trouvez et notez une estimation pour la position d'équilibre de la masse avec une précision de l'ordre du %.
• Écrivez un programme C qui affiche en deux colonnes x et f(x) pour un millier de points couvrant un intervalle que vous aurez choisi. Si vous pouvez, faites en sorte que le programme demande le paramètre G à l'utilisateur.
• Redirigez la sortie de ce programme dans un fichier
• Utilisez gnuplot pour afficher la liste de points. Se superposent-ils bien à la courbe analytique ?
• Écrivez un deuxième programme C qui cherche le zéro par dichotomie: partant de deux bornes a et b d'un intervalle tq f() change de signe entre a et b, on calcule la valeur de f au milieu de l'intervalle (f((a+b)/2)), et on remplace soit a soit b par (a+b)/2 de manière à garder le zéro dans le nouvel intervalle. On itère cette recette jusqu'à ce que ... réfléchissez à ce qu'on peut mettre comme condition d'arrêt! Vérification du programme: l'intervalle obtenu contient-il bien le zéro noté plus haut ?
• Comment peut-on améliorer cette recherche de zéro ? Réfléchissez à une manière intélligente de profiter de l'information dont on dispose (f(a), f(b) par exemple, mais aussi la dérivée f'(x),...?). Réalisez un troisième programme (peut-être juste une modification du deuxième) pour tester la convergence de votre méthode.