Allongement électrostatique d'un polymère
Description du modèle
On modélise un polymère par une chaîne linéaire de N atomes ou molécules (les monomères) reliés par des ressorts (assurant la cohésion de l'ensemble), de raideurs k et de longueur à vide l.
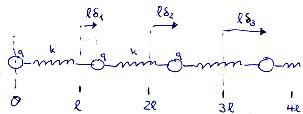
Lors de sa dissolution dans l'eau, les monomères se chargent positivement par échange d'électrons avec la solution. Tous les monomères sont alors supposés porter la même charge q, créant une force de répulsion électrostatique entre les monomères, et par conséquent un allongement du polymère.
La position du monomère n (n = 0,1,...,N-1) en dehors de la solution est xn* = n*l. Une fois en solution les monomères vont se décaler de cette position et trouve un nouvel équilibre à la position xn = xn* + lδn = l*(n+δn). Une translation du polymère entier ne change pas son équilibre, on peut donc considérer que le premier monomère est à l'origine: x0 = x0* = 0 (i.e. δ0 = 0).
- Écrire le bilan des forces pour un monomère à l'intérieur du polymère (1 ≤ n ≤ N-2). Notez que les forces électrostatiques sont à longue portée, alors que les ressorts modélisent des interactions covalentes entre voisins. On introduira le paramètre α = 4πε0 kl³/q² (rapport de la force de rappel à la force électrostatique).
En supposant les allongements relatifs entre deux monomères petits (|δi - δj| << |i - j|), linéarisez l'équation obtenue en utilisant 1/(1 + ε)² ~ 1 - 2ε.
Le calcul précédent (plus le bilan particulier pour le dernier monomère) conduit à un système d'équations linéaires pour les δn. Pour calculer les déplacements des monomères δn, on voit qu'il faut résoudre l'équation (αA + B)δ = C, où A et B sont des matrices (N-1)*(N-1), δ et C des vecteurs de dimension N-1, définis par:
Ci = s2(N - 1 - i) - s2(i), pour i = 1..N-1 avec s2(m) = ∑ j=1 m 1/j²
Ai,i = -2 pour i = 1..N-2 ; AN-1,N-1 = -1
Ai+1,i = Ai,i+1 = 1 pour i = 1..N-2
Ai,j = 0 sinon
Bi,i = -2 (s3(i) + s3(N - 1 - i)), pour i = 1..N-1 avec s3(m) = ∑ j=1 m 1/j³
Bi,j = 2/|j-i|³ pour i différent de j
Ecrire un programme calculant le vecteur des allongements relatifs δ = (δ2, δ3, ..., δN) pour α de l'ordre de 100. Vous pouvez utiliser ce squelette de programme comme point de départ.
Tracer la fonction d'étirement f(n) = δn - δn-1. Comment évolue l'étirement avec la taille N du polymère ?
Pour N=4, tracer l'étirement total du polymère δ3 en fontion de α.