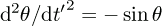• Accueil
• TD 1: gnuplot, C, dichotomie
• TD 2: Euler (modifié) [pendule]
  • Animation ECMAScript
  • Animation Java
  • Animation ActionScript/Flash
• TD 3: Euler implicite [pendule]
• TD 4: Runge-Kutta 4 [Bruxellateur]
• TD 5: EDP parabol [Chaleur]
• TD 6: EDP hyperbol [Tube à choc]
• TD 7: Equ linéaires [Polymère]
• TD 8: Nbres aléat., Monte-Carlo
• TD 9: Minimisation [points Lagrange]

• Documentation
• Unix
• C
• C++
• Java
• Python
• Comparatif langages
• Gnuplot
• Méthodes num.

• Nouvelles
• Notes de cours
• Enseignants

Intégration numérique d'une équation différentielle ordinaire: schéma d'Euler simple et modifié

Le but de ce TD est de programmer deux intégrateurs numériques d'EDO et de comparer leur précision.

Le problème

Nous allons traiter le mouvement d'un pendule rigide: une masse m est reliée à un pivot par une tige de longueur l, supposée rigide et de masse nulle. Le pendule se trouve dans un champ de pesanteur homogène g.

Pas à pas

• Écrivez l'équation dynamique pour l'angle que forme la tige avec la verticale.

• En remplacant le temps t par T*t', où T = sqrt(l/g) est la periode d'oscillation à petite amplitude et t' un temps sans dimension, montrez que l'équation sans dimension a la forme

  

  (nous écrivons de nouveau t à la place de t' dans la suite).

• Réécrivez cette équation d'ordre 2 comme un système d'équations d'ordre 1.
• Écrivez un programme en C qui intègre ce système d'équations par la méthode d'Euler (*), et qui affiche à chaque pas de temps le temps t, la position theta et la vitesse omega. Prenez comme conditions initiales une amplitude nulle et une vitesse de 0.5. Simulez de t = 0 à t = 50 en pas de h = 0.01. Si vous pouvez, faites en sorte que le programme demande ces grandeurs à l'utilisateur.
• Redirigez la sortie de ce programme dans un fichier
• Utilisez gnuplot pour afficher un graphe (t,theta) puis (theta,omega).
• Faites une deuxième simulation en multipliant le pas de temps par 10: h = 0.1. Qu'observez-vous ?
• Faites une troisième simulation en prenant comme vitesse initiale omega = 3. Qu'observez-vous ? Explorez d'autres conditions initiales.
• Écrivez un deuxième programme C (prenez le premier comme point de départ) qui utilise le schéma d'Euler modifié. Lancez des simulations avec les mêmes paramètres que précédemment et observez la différence.

(*) Voici un squelette de programme qui peut vous servir de point de départ, à compléter:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main(void) {
  float t, tfinal, h;
  float theta, omega, dtheta, domega;
  int i,npas;

  tfinal=5.0; // temps final
  h=0.01; // pas d'intégration
  theta=0.0;
  omega=0.5;

  npas = tfinal/h; // nombre de pas d'intégration


  // à compléter...


  return EXIT_SUCCESS;
}