Schéma de Runge-Kutta 4 pour l'intégration d'EDO
Réactions chimiques oscillantes
Jusqu'aux années 1950, on était convaincu que la thermodynamique n'admettait que des réactions chimiques qui tendraient vers un équilibre de manière monotone. Depuis les travaux de B. Belousov et quelques années plus tard A. M. Zhabotinskii, on connait plusieurs mélanges d'espèces chimiques qui réagissent de manière oscillante, montrant donc des variations périodiques de concentration et de propriétés physiques (densité optique, potentiels électriques, ...). Nous allons étudier la dynamique du Bruxellateur, un système hypothétique modèle de réaction chimique à plusieurs composants. [ quelques détails supplémentaires sur les motifs dans les réactions chimiques ici, et plus particulièrement sur le Bruxellateur ici ]
Le système complet fait réagir 6 espèces A,B,C,D,X,Y selon les réactions suivantes:
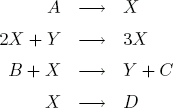
L'espèce A n'intervient que dans la première réaction, où elle produit X. De manière symétrique, la dernière équation décrit la destruction de X en D. Les deux réactions intéressantes sont la troisième, bi-moléculaire, et la deuxième, tri-moléculaire mais surtout auto-catalytique. Il faut se rappeler que la plupart des réactions chimiques a lieu à un taux qui est proportionnel à la concentration des réactants, donc par exemple dA/dt = -V1 A = -dX/dt, où A dénote la concentration du réactant A, et V1 est la vitesse de la première réaction. La deuxième réaction produit donc X d'autant plus vite qu'il y a déjà de X: dX/dt = V2 X² Y; c'est cette propriété qu'on appelle auto-catalytique. Cependant X intervient dans toutes les équations, de sorte que d'autres termes interviennent dans son équation d'évolution:
dA/dt = - V1 A
dB/dt = - V3 B X
dC/dt = + V3 B X
dD/dt = + V4 X
dX/dt = + V1 A + V2 X² Y - V3 B X - V4 X
dY/dt = - V2 X² Y + V3 B X
On étudiera le cas particulier où A est présent en quantité inépuisable et B est injecté à la vitesse v.
L'étude pas à pas
-
Notant Z la concentration de B pour faire plus joli, et posant A = 1, V1 = V2 = V3 = V4 = 1, montrez que la dynamique de réaction est décrite par le système de trois équations suivantes:
X' = 1 - (Z+1) X + X² Y Y' = X Z - X² Y Z' = - X Z + v -
Écrivez un programme C qui résoud numériquement ce système en utilisant un schéma Runge-Kutta d'ordre 4 pour l'intégration. Intégrez le système pour les valeurs de v suivantes: 0.9, 1.3 et 1.52, et différentes conditions initiales. Dans chaque cas, tracez d'une part les trois concentrations X, Y et Z en fonction du temps, puis deux concentrations en fonction de la troisième.
k1 = dt * f(tn, yn)
k2 = dt * f(tn + dt/2, yn + k1/2)
k3 = dt * f(tn + dt/2, yn + k2/2)
k4 = dt * f(tn + dt, yn + k3)
yn+1 = yn + (k1 + 2 k2 + 2 k3 + k4)/6