Corrigé de l'examen janvier 2005

Réponse à la question 1

En notant u=dx/dt et v=dy/dt les vitesses, on passe à un système de quatre équations d'ordre 1 pour les quatre quantités (x, y, u, v): 

dx/dt = u
dy/dt = v
du/dt = 2 v + x - (1-μ) (x+μ)/rS³ - μ (x-1+μ)/rJ³
dv/dt = -2 u + y - (1-μ) y/rS³ - μ y/rJ³

Le paramètre d'intégration est le temps.

Réponse à la question 2

La fonction main() du programme troiscorps.c suivant

Quelques fonctions sont définies séparément avant le main(). 

#include <stdio.h>
#include <math.h>

double mu;

/* calcul de la distance P-J */
double rj(double *X) {
  return sqrt((X[0]-1+mu)*(X[0]-1+mu) + X[1]*X[1]);
}

/* calcul de la distance P-S */
double rs(double *X) {
  return sqrt((X[0]+mu)*(X[0]+mu) + X[1]*X[1]);
}

/* distance P-J au cube */
double rj3(double *X) {
  double r;
  r = rj(X);
  return r*r*r;
}

/* distance P-S au cube */
double rs3(double *X) {
  double r;
  r = rs(X);
  return r*r*r;
}

/* calcul de la dérivée pour l'intégration RK4 */
void deriv(double *X, double *k, double dt) {
  k[0] = dt*X[2];
  k[1] = dt*X[3];
  k[2] = dt*(2*X[3] + X[0] - (1-mu)*(X[0]+mu)/rs3(X) - mu*(X[0]-1+mu)/rj3(X));
  k[3] = dt*(-2*X[2]+ X[1] - (1-mu)*X[1]/rs3(X) - mu*X[1]/rj3(X));
  return;
}

/* calcul de l'énergie du système */
double energie(double* X) {
  return 0.5*(X[2]*X[2]+X[3]*X[3]) - (1-mu)/rs(X) - mu/rj(X)
    - 0.5*(X[0]*X[0]+X[1]*X[1]);
}

int main(void) {
  /* déclaration des variables */
  double X[4], Xt[4], k1[4], k2[4], k3[4], k4[4];
  int n,npas,i;
  double t, tmax, dt, E;

  /* Initialiser les parametres suivants :
    tmax = temps final
    dt= pas de temps
    mu = rapport des masses de J et S
  */

  t = 0;
  tmax = 1000;
  dt = 0.001;
  mu = 0.001;

  /* Initialiser les conditions initiales, les composantes
     du vecteur X ont la signification suivante:
   X(0) = X
   X(1) = Y
   X(2) = Vx
   X(3) = Vy
  */

  X[0] = 0.5-mu+0.002;
  X[1] = sqrt(3.0)/2;
  X[2] = 0.01;
  X[3] = 0.01;

  /* calculer le nombre de pas d'intégration */
  npas=tmax/dt;
  /* calculer et afficher l'énergie initiale */
  E = energie(X);
  printf("%f %f %f %f %f %f\n",t,X[0],X[1],X[2],X[3],E);

  /* boucle d'intégration */
  for (n=0; n<npas ; n++) {
    /* pas d'intégration Runge/Kutta 4 */
    deriv(X,k1,dt);
    for (i=0; i<4; i++) { Xt[i] = X[i] + 0.5*k1[i]; }
    deriv(Xt,k2,dt);
    for (i=0; i<4; i++) { Xt[i] = X[i] + 0.5*k2[i]; }
    deriv(Xt,k3,dt);
    for (i=0; i<4; i++) { Xt[i] = X[i] + k3[i]; }
    deriv(Xt,k4,dt);
    for (i=0; i<4; i++) { X[i] += (k1[i] + 2*k2[i] + 2*k3[i] + k4[i])/6; }
    /* nouvelle valeur de l'énergie ? */
    E = energie(X);
    t = (n+1)*dt;
  }

  /* afficher l'énergie à la fin de l'intégration */
  printf("%f %f %f %f %f %f\n",t,X[0],X[1],X[2],X[3],E);
  return 0;
}

Réponse à la question 3

Le programme est compilé en invoquant le compilateur gcc: 

ordi:~ $ gcc -W -Wall troiscorps.c -lm -o troiscorps

l'executable est lancé en tapant son nom: 

ordi:~ $ ./troiscorps

Réponse à la question 4

Sur une machine donnée, le programme précédent (avec les bonnes conditions initiales) donne:

htxyuvE
0.0000000.7000000.7000000.1000000.100000-1.489736
0.01100.0-0.176151-1.075074-0.1304030.160889-1.489736
0.1100.0-0.162942-1.089444-0.1554030.158440-1.489736
1.0100.0-1.078834-0.541112-0.2662540.218691-1.497782

On voit que même avec le pas le plus grand, h=1.0, l'erreur reste en dessous de 1%. De ce point de vue il n'y a donc pas de raison de prendre un pas plus faible.

La position ou la vitesse finale cependant est très différente ce celle obtenue pour un pas de temps plus faible. Si on exige ici aussi un erreur inférieur au %, même un pas de 0.1 n'est pas suffisamment faible. Si on prend l'écart à la position obtenue pour h=0.01 comme ordre de grandeur pour la vraie déviation, on voit qu'elle est d'environ 10% pour h=0.1. On peut espérer gagner bien plus d'un facteur 10 sur la précision en divisant le pas de temps par 10 dans un schéma d'ordre 4: h=0.01 devrait donc être suffisamment précis.

Réponse à la question 5

La seule modification à apporter au programme troiscorps.c consiste à déplacer le deuxième printf() à l'interieur de la boucle for (à la fin, après le calcul du temps), c'est-à-dire de le remonter de quatre lignes.

Les graphes suivants montrent qu'on peut prendre h=1.0 ou même plus grand, si le seul critère est d'avoir moins de 1% d'erreur sur l'énergie.

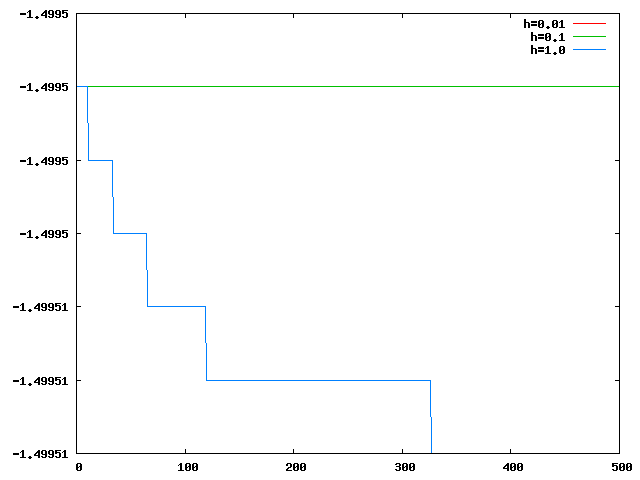
Libration: energie(t)

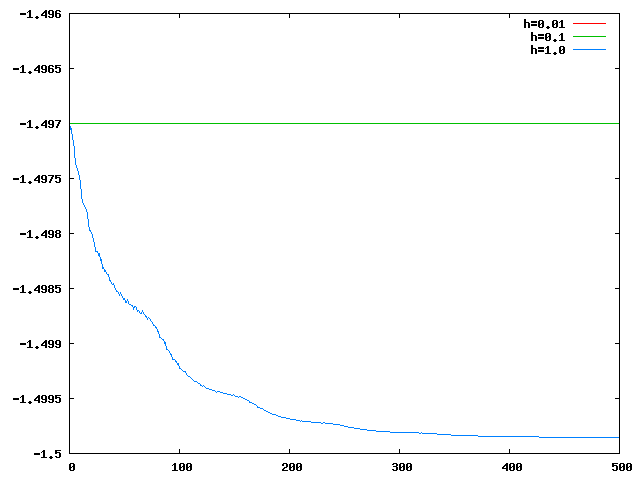
Circulation: energie(t)

On voit cependant que l'énergie n'est constante que pour h<=0.1.

Réponse à la question 6

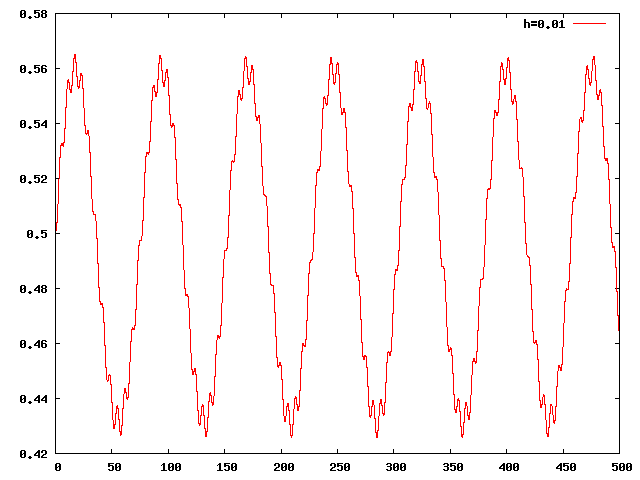
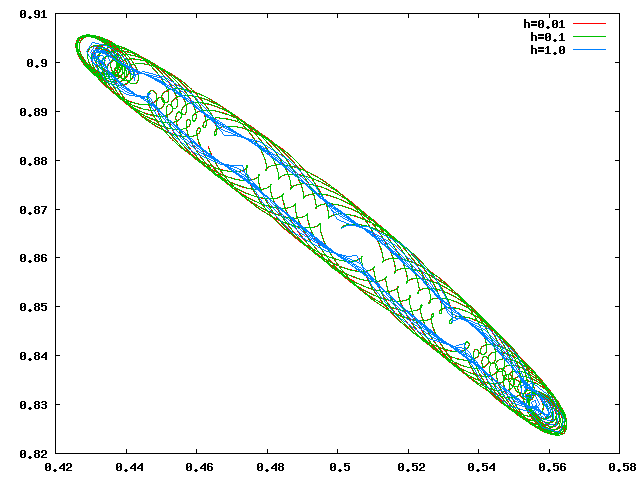
Libration orbite (x(t),y(t))

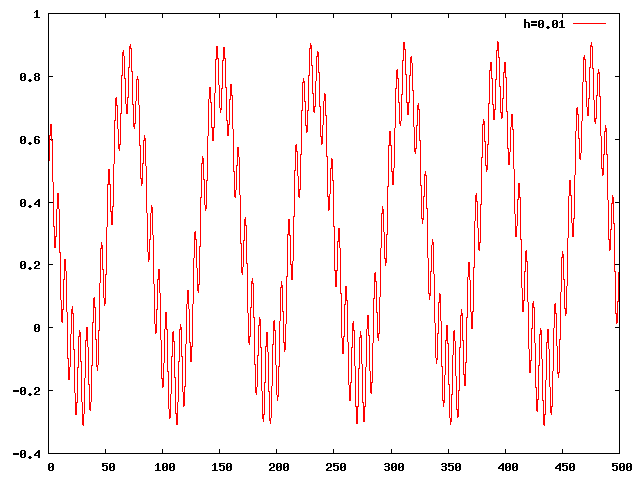
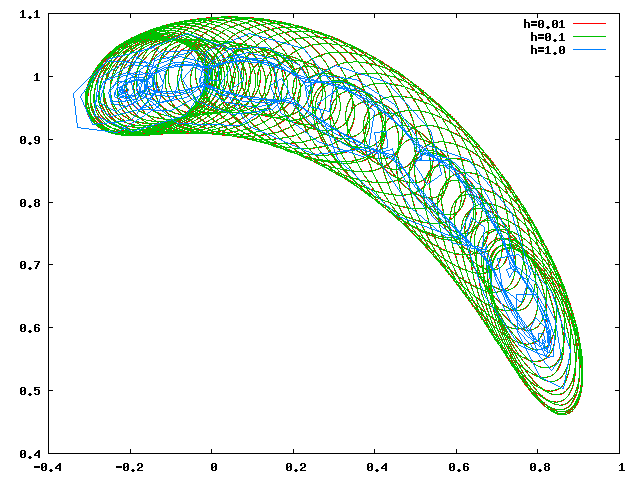
Circulation orbite (x(t),y(t))

Les orbites de libration et de circulation calculées avec h=0.1 et h=0.01 se superposent, il est donc raisonnable de penser que h=0.1 est suffisant.

Réponse à la question 7

  1. La libration a une période d'envion 76+-0.4 unités de temps. Ceci est beaucoup (environ 12 fois) plus grand que la durée de l'année Jupiterienne. x(t)
  2. Il n'y a pas d'oscillation autour de Jupiter (on a toujours y(t)>1). Il y a rapprochement maximal toutes les 80 unités de temps. Pendant cette période, le corps oscille environ 12 fois autour de l'orbite de Jupiter. x(t)

Réponse à la question 8

Modification du programme stabilite.c: Une boucle for autour de l'initialisation et de l'intégration nous permet de lancer la simulation N fois. L'initialisation se sert d'une fonction alea() pour tirer les conditions initiales au hasard. La boucle d'intégration peut être réduite au stricte minimum, il ne faut afficher qu'une fois la position à la fin de l'intégration. 

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

double mu;

double rj(double *X) {
  return sqrt((X[0]-1+mu)*(X[0]-1+mu) + X[1]*X[1]);
}

double rs(double *X) {
  return sqrt((X[0]+mu)*(X[0]+mu) + X[1]*X[1]);
}

double rj3(double *X) {
  double r;
  r = rj(X);
  return r*r*r;
}

double rs3(double *X) {
  double r;
  r = rs(X);
  return r*r*r;
}

void deriv(double *X, double *k, double dt) {
  k[0] = dt*X[2];
  k[1] = dt*X[3];
  k[2] = dt*(2*X[3] + X[0] - (1-mu)*(X[0]+mu)/rs3(X) - mu*(X[0]-1+mu)/rj3(X));
  k[3] = dt*(-2*X[2]+ X[1] - (1-mu)*X[1]/rs3(X) - mu*X[1]/rj3(X));
  return;
}

double energie(double* X) {
  return 0.5*(X[2]*X[2]+X[3]*X[3]) - (1-mu)/rs(X) - mu/rj(X)
    - 0.5*(X[0]*X[0]+X[1]*X[1]);
}

double alea() {
  return ((double)rand()/(RAND_MAX+1.0));
}

int main(void) {
  double X[4], Xt[4], k1[4], k2[4], k3[4], k4[4];
  int n,npas,i,m;
  double t, tmax, dt, E;
  double r,a,v;

for (m=0; m<10000; m++) {

  /* Initialiser les parametres suivants :
    tmax = temps final
    dt= pas de temps
    mu = rapport des masses de J et S
  */

  t = 0;
  tmax = 100;
  dt = 0.1;
  mu = 0.01;

  /* Tirer les conditions initiales au hasard */

  r = 0.7+0.6*alea();
  a = 2*M_PI*alea();
  v = 1/sqrt(r*r*r) - 1;

  X[0] = r*cos(a);
  X[1] = r*sin(a);
  X[2] = -v*sin(a);
  X[3] = v*cos(a);

  npas=tmax/dt;
  for (n=0; n<npas ; n++) {
    deriv(X,k1,dt);
    for (i=0; i<4; i++) { Xt[i] = X[i] + 0.5*k1[i]; }
    deriv(Xt,k2,dt);
    for (i=0; i<4; i++) { Xt[i] = X[i] + 0.5*k2[i]; }
    deriv(Xt,k3,dt);
    for (i=0; i<4; i++) { Xt[i] = X[i] + k3[i]; }
    deriv(Xt,k4,dt);
    for (i=0; i<4; i++) { X[i] += (k1[i] + 2*k2[i] + 2*k3[i] + k4[i])/6; }
  }

  E = energie(X);
  t = n*dt;
  printf("%f %f %f %f %f %f\n",t,X[0],X[1],X[2],X[3],E);
}
  return 0;
}

Les positions finales forment la distribution suivante:

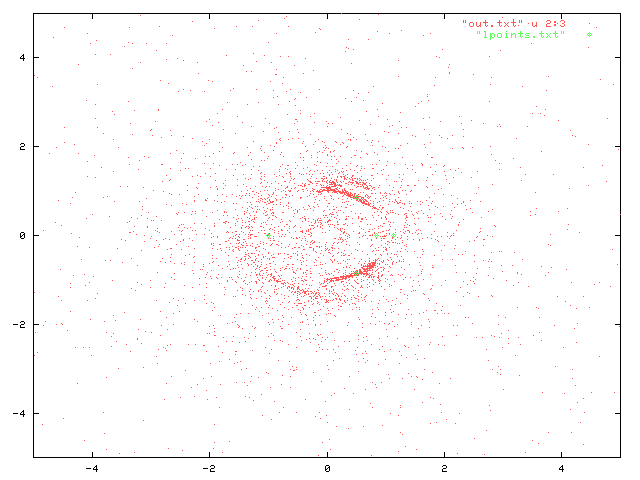
nuage d'asteroides

Dans ce graphe, les points verts représentent les points de Lagrange pour notre configuration: 

0.5 0.866
0.5 -0.866
1.14 0.0
0.84 0.0
-1.0 0.0

On peut constater que nos particules tests sont particulièrement denses autour de L4 et L5. Aucune accumulation n'est en revanche visible près des points L1, L2 et L3. Quelques structures plus faibles (et pas symétriques par rapport à l'axe Soleil-Jupiter) sont visibles: il faudrait verifier par d'autres tirages s'il s'agit de fluctuations ou pas.

Auteur(s) : A. Daerr. Dernière modification : Sat Oct 25 19:59:42 2008. [validate XHTML]