Corrigé de l'examen janvier 2007
Réponse à la question 1
En un lapse de temps dt, une quantité de combustible
dm=β*dt est ejectée de la fusée. Le gaz est ejecté à
vitesse vg par rapport à la fusée, et emporte
donc une quantité de mouvement dp =
(vfusee+vg)*dm dans un
référentiel non-accéléré. Par réaction, la quantité de mouvement de la
fusée augmente de dp dans le sens opposé. La variation de la quantité
de mouvement par unité de temps est donc dp/dt = -
β*(vfusee+vg). Le terme
β*vfusee correspond simplement à la
perte de poids (il serait encore là si on largait le carburant à
vitesse nulle), la poussée du moteur correspond au terme
supplémentaire β*vg.
Autrement dit (plus formellement): la somme des impulsions de la fusée
et des produits de combustion est conservée (dans un référentiel
non-accéléré en l'absence de gravitation, ou plus généralement dans le
référentiel du centre de masse), donc
d(pfusee+pgaz)/dt =
0. La quantité de mouvement pgaz
augmente uniquement par la quantité de mouvement des gaz fraîchement
éjectés (à une vitesse
vfusee+vg par rapport
à notre référentiel). On a donc dpgaz/dt =
β*(vfusee+vg) pour le
second terme:
dpfusee/dt + β*(vfusee+vg) = 0
En dérivant la quantité de mouvement de la fusée,
pfusee = mvfusee, il
faut bien se rappeler qu'aussi bien la masse que la vitesse dépendent
du temps:
d(pfusee+pgaz)/dt = dm/dt vfusee + m dvfusee/dt + β*(vfusee+vg) = 0
Le changement de masse de la fusée est juste dm/dt =
-β. L'équation devient donc:
m dvfusee/dt + β vg = 0
Réponse à la question 2
En ajoutant la gravitation à droite dans l'équation qui précède, on arrive à:
m dvfusee/dt = - (G Mterre m/r²) ur - β vg
G est la constante de gravitation, et
ur un vecteur unitaire radial. On peut
réécrire cette expression en notant que l'accélération terrestre à la
surface vaut g = GMterre/R² et que la vitesse
d'éjection des produits de combustion se fait à un angle
α par rapport à la verticale (selon {-cos(φ+α),-sin(φ+α)}
donc). Si (r,φ) est la position de la fusée en
coordonnées cylindriques, on obtient alors pour les composantes selon
x et y de la vitesse (toujours de la fusée):
dvx/dt = - g/(r/R)² cos(φ) + β/m vg cos(φ+α) dvx/dt = - g/(r/R)² sin(φ) + β/m vg sin(φ+α)
Réponse à la question 3
En notant u=dx/dt et v=dy/dt les vitesses, on peut réécrire les deux équations du mouvement d'ordre 2 comme quatre équations du premier ordre. En y ajoutant l'équation d'évolution de la masse de la fusée on obtient le système suivant de cinq équations pour les quantités (x, y, u, v, m):
dx/dt = u dy/dt = v du/dt = - cos(φ)/r² + cos(φ+α)*poussee/m; dv/dt = - sin(φ)/r² + sin(φ+α)*poussee/m; dm/dt = - β
(où bien évidemment r(x,y) et φ(x,y) sont des fonctions)
Le paramètre d'intégration est le temps.
Réponse à la question 4
Seule l'équation d'évolution de la masse doit être modifiée une fois le carburant épuisé. La masse de la fusée ne change plus, la cinquième équation devient donc triviale:
dx/dt = u dy/dt = v du/dt = - cos(φ)/r² + cos(φ+α)*poussee/m; dv/dt = - sin(φ)/r² + sin(φ+α)*poussee/m; dm/dt = 0
Réponse à la question 5
Voici un programme qui simule le vol de la fusée: [ voir fusee.c | télécharger
fusee.c ]. Ce programme a été réalisé à partir de la solution du
TD sur le Bruxellateur, bruxellateur_rk4_deluxe.c. Les changements
concernent les conditions initiales (la vitesse initiale de la fusée
est prise égale à la vitesse tangentielle de l'équateur, calculée à
partir de la durée du jour: 2π/110 = 0.058), les équations
d'évolution, et deux tests dans la boucle d'intégration pour savoir si
le carburant est épuisé ou pas, et si la fusée se trouve toujours au
dessus de la surface de la terre. Voici ce qu'il a fallu modifier
pour adapter le programme mentionné à la fusée (les parties précédées d'un '-' ont
été effacées, les parties précédées d'un
'+' ajoutées):
ordi:~ $ diff -u brusselator_rk4_deluxe.c fusee.c --- brusselator_rk4_deluxe.c 2006-10-22 20:06:29.000000000 +0200 +++ fusee.c 2007-02-05 07:12:26.000000000 +0100 @@ -1,37 +1,60 @@ -/* Bruxellateur, version modularisee */ -/* les variables X,Y,Z du modele sont stockees dans les tableaux selon - la correspondance: - X <-> S[0] - Y <-> S[1] - Z <-> S[2] +/* Trajectoire fusee */ +/* (examen physique numerique janvier 2007) */ +/* les variables x,y,vx,vy,m du modele sont stockees dans les + tableaux selon la correspondance: + x <-> S[0] + y <-> S[1] + vx <-> S[2] + vy <-> S[3] + m <-> S[4] */ #include <stdio.h> #include <stdlib.h> +#include <math.h> // nombre de variables d'etat (=nombre d'equations d'evolution) -#define NEQ 3 +#define NEQ 5 -double v=1.52; +double alpha = 60/*deg*/ *(M_PI/180); /* inclinaison fusee par rapport + à la verticale */ +double carburant = 0.97; /* fraction initiale carburant */ +double poussee = 1.6; /* poussee moteur initiale en g */ +double combust = 4; /* taux de combustion (-dm/dt)*/ +int vollibre = 0; /* 0: avec moteur, >0: vol libre */ /* conditions initiales de notre probleme */ void init(double *S) { - S[0]=1; - S[1]=2; - S[2]=1; + S[0]=1;// surface de la terre + S[1]=0; + S[2]=0; + S[3]=0.058;// vitesse tangentielle de l'equateur + S[4]=1; } /* Cette fonction contient toute la physique: les equations d'evolution sont utilisees pour calculer le changement d'etat dS a partir de l'etat S */ void derive(double *S, double* dS) { - dS[0] = 1 - (S[2]+1)*S[0] + S[0]*S[0]*S[1]; - dS[1] = S[0]*S[2] - S[0]*S[0]*S[1]; - dS[2] = - S[0]*S[2] + v; + double r2,phi; //coordonnees cylindriques + r2 = S[0]*S[0]+S[1]*S[1]; + phi = atan2(S[1],S[0]); + //printf("%f %f\n",r2,phi); + dS[0] = S[2]; + dS[1] = S[3]; + if (vollibre == 0) {// encore du carburant ? + dS[2] = - cos(phi)/r2 + cos(phi+alpha)*poussee/S[4]; + dS[3] = - sin(phi)/r2 + sin(phi+alpha)*poussee/S[4]; + dS[4] = -combust; + } else {// sinon vol libre + dS[2] = - cos(phi)/r2; + dS[3] = - sin(phi)/r2; + dS[4] = 0; + } } @@ -69,7 +92,7 @@ // fichier pour la description des elements) double S[NEQ]; // intervalle d'integration [t,tmax] et pas d'integration - double t=0, tmax=30, dt=0.01; + double t=0, tmax=100, dt=0.001; // compteur de pas, nombre de pas d'integration int n,nmax; nmax = (tmax-t)/dt; @@ -79,12 +102,22 @@ for (n=0; n<nmax ; n++) { t = n*dt; // afficher l'état actuel - printf("%lf %lf %lf %lf\n",t,S[0],S[1],S[2]); + printf("%lf %lf %lf %lf %lf %lf\n",t,S[0],S[1],S[2],S[3],S[4]); // integrer d'un pas de temps dt rk4(S,dt); + // verifier si nous avons encore du carburant + if ((vollibre==0) && (S[4] < 1-carburant)) { + vollibre = 1; + dt = 100*dt; + } + // verifier si on est retombe sur la terre + if ((vollibre>0) && (S[0]*S[0]+S[1]*S[1] <= 1)) { + printf("# crash!"); + break; + } } // affichage de l'état final t = n*dt; - printf("%lf %lf %lf %lf\n",t,S[0],S[1],S[2]); + printf("%lf %lf %lf %lf %lf %lf\n",t,S[0],S[1],S[2],S[3],S[4]); return EXIT_SUCCESS; }
Le programme est compilé en invoquant le compilateur gcc:
ordi:~ $ gcc -W -Wall fusee.c -lm -o fusee
l'executable est lancé en tapant son nom:
ordi:~ $ ./fusee
Réponse à la question 6
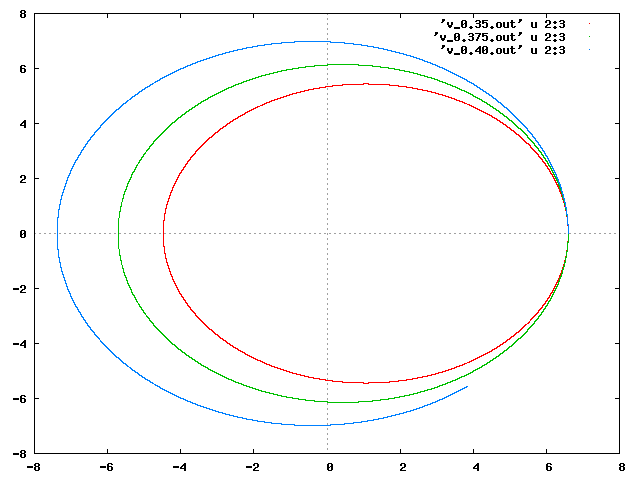
La simulation a été lancée pour une fusée sans carburant lancée à 6.6 unités du centre de la terre avec une vitesse tangentielle de 0.35, 0.375 et 0.4. Les orbites (x(t),y(t)) montrent que la trajectoire devrait être circulaire pour une vitesse initiale située entre 0.375 et 0.4.
Réponse à la question 7
Il est clair que le pas de temps doit être très court devant le temps
de combustion, qui vaut ici 1/4. Un pas de 0.001 ne semble cependant
pas encore suffisamment petit (voir graphique montrant les
trajectoires pour des pas de 1e-3, 1e-4 et 1e-5): la trajectoire se
distingue encore clairement des trajectoires pour des pas de temps
plus petits. Celles pour 1e-4 et 1e-5 se confondent presque. Le pas ne
doit donc pas être choisi plus grand qu'environ 1e-4 ou 1e-5. 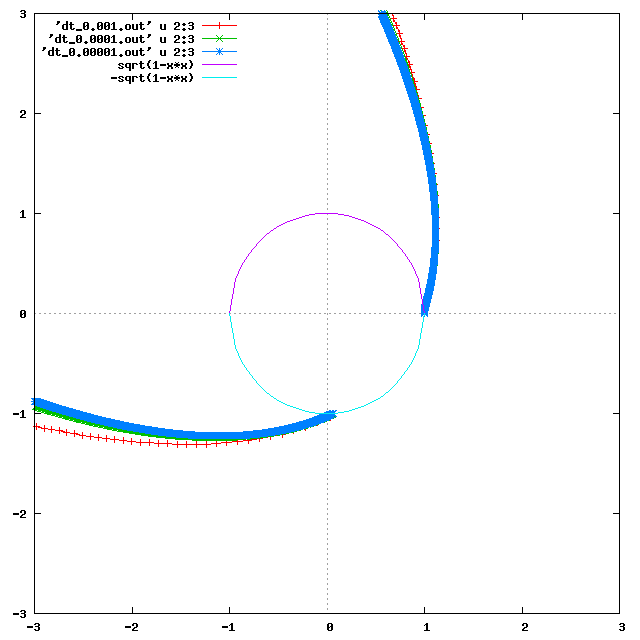
Réponse à la question 8
On peut soit modifier le programme pour relancer la simulation avec différents angles de tirs, et vérifier si la fusée revient à la surface de la terre (comme c'était la cas à la question 7), soit faire le travail à la main. Il semble qu'il n'existe pas (avec les conditions initiales de la question 7) d'angle de tir qui permette d'obtenir une orbite. C'est cependant possible en augmentant par exemple la fraction de carburant.